tìm m để phương trình có nghiệm thỏa mãn
\(x^2-mx+m+1=0\)thỏa mãn x1x2+2(x1+x2)-19=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
Để pt có 2 nghiệm thì:
\(\left\{\begin{matrix} m\neq 0\\ \Delta'=(m+1)^2-m(m+5)=1-3m\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ m\leq\frac{1}{3}\end{matrix}\right.(1)\)
Áp dụng định lý Viet:
\(\left\{\begin{matrix} x_1+x_2=\frac{2(m+1)}{m}\\ x_1x_2=\frac{m+5}{m}\end{matrix}\right.\)
Để $x_1< 0< x_2$
$\Leftrightarrow x_1x_2< 0$
$\Leftrightarrow \frac{m+5}{m}< 0$
$\Leftrightarrow -5< m< 0(2)$
$x_1< x_2< 2$
\(\Leftrightarrow \left\{\begin{matrix} (x_1-2)(x_2-2)>0\\ x_1+x_2<4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_1x_2-2(x_1+x_2)+4>0\\ x_1+x_2<4\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{m+1}{m}>0\\ \frac{1-m}{m}< 0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m>1\\ m< -1\end{matrix}\right.(3)\)
Từ $(1);(2);(3)$ suy ra $-5< m< -1$
10 tháng 3 2021
Ta có: \(\Delta\) = m2 - 4(m - 1) = m2 - 4m + 4 = (m - 2)2 \(\ge\) 0
\(\Rightarrow\) x1 = \(\dfrac{m-\left(m-2\right)}{2}=1\); x2 = \(\dfrac{m+m-2}{2}=m-1\)
Ta có: |x1| + |x2| = 4
\(\Leftrightarrow\) 1 + |m - 1| = 4
\(\Leftrightarrow\) |m - 1| = 3
\(\Leftrightarrow\) \(\left[{}\begin{matrix}m-1=3\\m-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)
Vậy ...
Chúc bn học tốt!
CM
15 tháng 12 2018
Đáp án B
Điều kiện: x > 0. Đặt t = log3x, khi đó phương trình trở thành t2 - (m+2)t + 3m - 1 = 0 (*)
Để phương trình có có hai nghiệm <=> (*) có 2 nghiệm phân biệt
Khi đó, gọi t1, t2 là hai nghiệm phân biệt của (*) theo hệ thức Viet, ta có
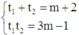
Theo bài ra, có
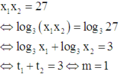
Đối chiếu điều kiện (m+2)2 - 4(3m - 1) > 0 suy ra m = 1 là giá trị cần tìm
CM
27 tháng 6 2019
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
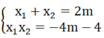
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
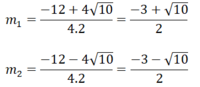
Vậy với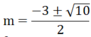 
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
28 tháng 3 2023
x1^2+x2^2=(x1+x2)^2-2x1x2
=m^2-2(m-1)=m^2-2m+2
=>x1^2=m^2-2m+2-x2^2
x1^2+3x2=19
=>m^2-2m+2-x2^2+3x2=19
=>-x2^2+3x2+m^2-2m-17=0
=>x2^2-3x2-m^2+2m+17=0(1)
Để (1) có nghiệm thì Δ1>0
=>(-3)^2-4*1*(-m^2+2m+17)>0
=>9-4(-m^2+2m+17)>0
=>9+4m^2-8m-68>0
=>4m^2-8m-59>0
=>\(\left[{}\begin{matrix}m< \dfrac{2-3\sqrt{7}}{2}\\m>\dfrac{2+3\sqrt{7}}{2}\end{matrix}\right.\)
2 tháng 4 2021
c) Ta có: \(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(2m+1\right)\)
\(=\left(-2m-2\right)^2-4\left(2m+1\right)\)
\(=4m^2+8m+4-8m-4\)
\(=4m^2\ge0\forall m\)
Do đó, phương trình luôn có nghiệm
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{1}=2m+2\\x_1\cdot x_2=2m+1\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1-2x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2=2m-1\\x_1=2m+2+x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{2m-1}{3}\\x_1=2m+3+\dfrac{2m-1}{3}=\dfrac{8m+8}{3}\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=2m+1\)
\(\Leftrightarrow\dfrac{2m-1}{3}\cdot\dfrac{8m+8}{3}=2m+1\)
\(\Leftrightarrow\left(2m-1\right)\left(8m+8\right)=9\left(2m+1\right)\)
\(\Leftrightarrow16m^2+16m-8m-8-18m-9=0\)
\(\Leftrightarrow16m^2-10m-17=0\)
\(\text{Δ}=\left(-10\right)^2-4\cdot16\cdot\left(-17\right)=1188\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{10-6\sqrt{33}}{32}\\m_2=\dfrac{10+6\sqrt{33}}{32}\end{matrix}\right.\)
cái này chỉ cần theo viet sau đó thay vào là ra thôi mà có cần biế đổi gì đâu
theo định lí vi ét: x1+x2=m
x1x2=m+1.
thay vào x1x2+2(x1+x2)-19=0, ta đc: m+1+2m-19=0=> m=18/3