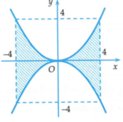
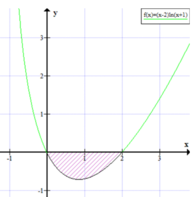
Trong mặt phẳng tọa độ Oxyz, gọi H 1 là hình phẳng giới hạn bởi các đường y = x 2 4 , y = − x 2 4 , x = − 4 , x = 4
và H 2 là hình gồm tất cả các điểm (x,y) thỏa x 2 + y 2 ≤ 16 , x 2 + ( y − 2 ) 2 ≥ 4 , x 2 + ( y + 2 ) 2 ≥ 4.
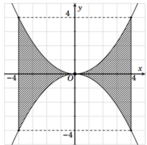
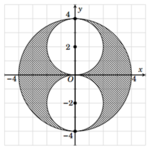
Cho H 1 và H 2 quay quanh trục Oy ta được các vật thể có thể tích lần lượt là V 1 , V 2 . Đẳng thức nào sau đây đúng?
A. V 1 = 1 2 V 2 .
B. V 1 = V 2 .
C. V 1 = 2 3 V 2 .
D. V 1 = 2 V 2 .

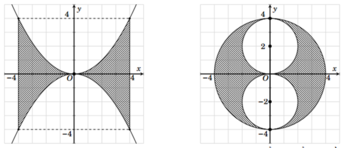
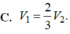
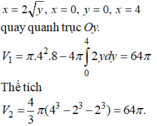


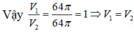

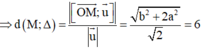
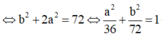
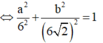
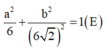
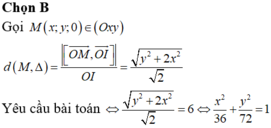
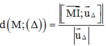
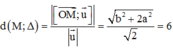
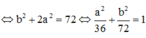
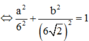
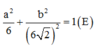
Đáp án B
V 1 bằng thể tích khối trụ có bán kính đáy bằng 4 và chiều cao bằng 8 trừ bốn lần thể tích của vật tròn xoay tạo thành khi vật thể giới hạn bởi các đường x = 2 y , x = 0 , y = 0 , x = 4 quay quanh trục Oy
. V 1 = π .4 2 .8 − 4 π ∫ 0 4 2 y d y = 64 π . Thể tích
V 2 = 4 3 π ( 4 3 − 2 3 − 2 3 ) = 64 π .