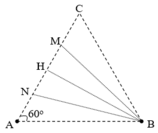
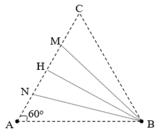
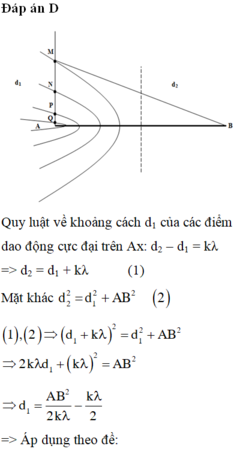
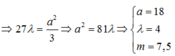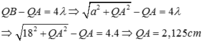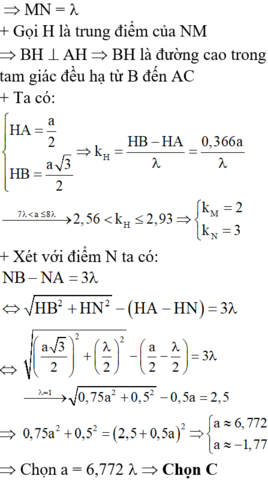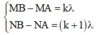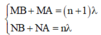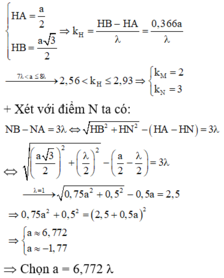Ở mặt chất lỏng có 2 nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm; NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây ?
A. 1,2 cm
B. 4,2 cm.
C. 3,1 cm
D. 2,1 cm.


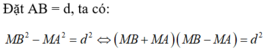
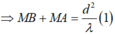
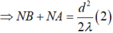
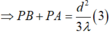

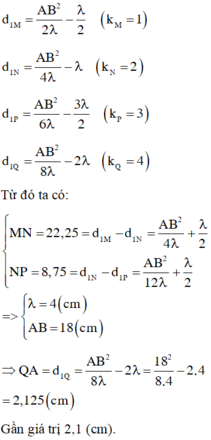

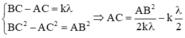
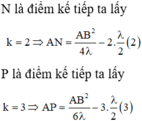
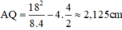


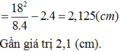
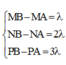
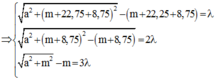
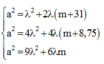
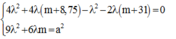
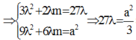
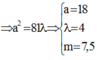

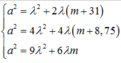 nên
nên