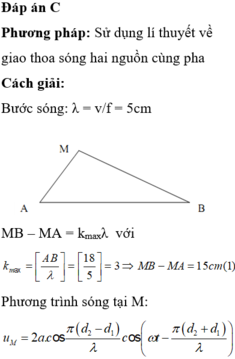
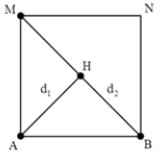
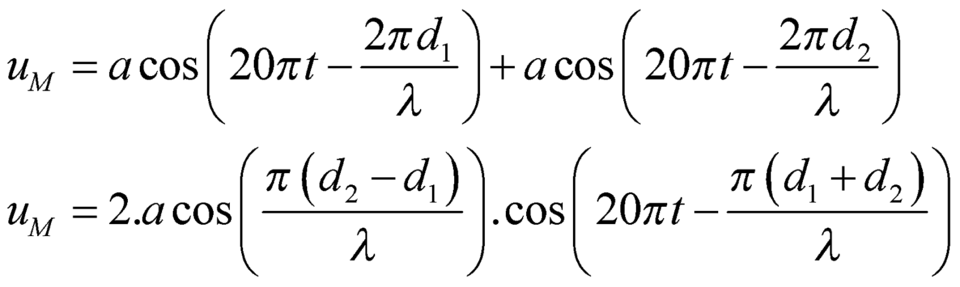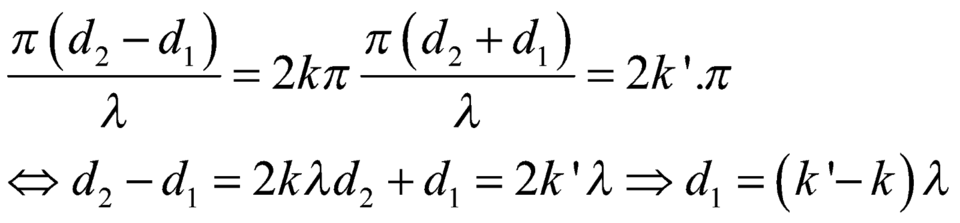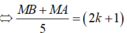Ở mặt thoáng của chất lỏng có hai nguồn sóng S 1 , S 2 cách nhau 18cm, dao động theo phương thẳng đứng với phương trình ( t tính bằng giây). Tốc độ truyền sóng trên mặt chất lỏng là 50cm/s. gọi M là điểm ở mặt chất lỏng gần S 1 nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha vơi nguồn S 1 . Khoảng cách AM là?
A. 1,25cm
B. 2,5cm
C. 5cm
D. 2cm