Gieo một con súc sắc năm lần liên tiếp. Xác suất để tích các số chấm xuất hiện ở năm lần gieo đó là một số tự nhiên có tận cùng bằng 5 là
A. 1 2
B. 211 7776
C. 2 3
D. 5 486
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 7 2017
Chọn C
Không gian mẫu: “ gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp”
Biến cố A: “ số a b c ¯ chia hết cho 45”
a b c ¯ chia hết cho 45 ⇔ a b c ¯ chia hết cho cả 5 và 9
Vì
a
b
c
¯
chia hết cho 5 nên 
là số chấm xuất hiện của súc sắc khi gieo).
Vì a b c ¯ chia hết cho 9 mà c = 5 => a + b + 5 chia hết cho 9.
Các cặp số (a;b) sao cho 
mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
Do đó: n(A) = 3.
CM
19 tháng 1 2019
Chọn C
Số phần tử của không gian mẫu của phép thử gieo một con súc sắc hai lần liên tiếp là 36.
Để phương trình bậc hai
x
2
+ bx + c = 0 có nghiệm là 
(*) với 
Gọi A là biến cố chọn cặp số (b;c) thỏa mãn 
trong đó 
Khi c = 1: Các giá trị của b thỏa mãn điều kiện (*) là: 2,3,4,5,6. Suy ra có: 5 cặp (b,c).
Khi c = 2: Các giá trị của b thỏa mãn điều kiện (*) là: 3,4,5,6. Suy ra có: 4 cặp (b,c).
Khi c = 3: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 4: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 5: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Khi c = 6: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Vậy, số cặp (b,c) thỏa mãn điều kiện (*) là 19
CM
13 tháng 10 2017
Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với 
⇒ 
⇒ 
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
.
.
.
.
CM
10 tháng 12 2017
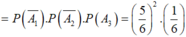
Đáp án C
Nhắc lại: xác suất của biến cố A được định nghĩa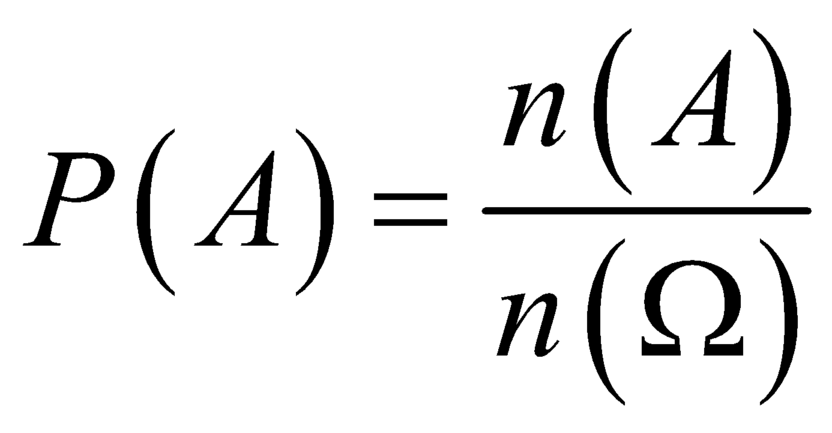 
, với 
là số phần tử của A, 
là số các kết quả có thể xảy ra của phép thử. Số phần tử của không gian mẫu là 
.
Gọi A là biến cố 
, ta có
A={(1;1) ;..(1;6); (2;2);..;(2;6);(3;3);..; (3;6); (4;5); (4;6)}
Suy ra 
. Vậy xác suất để phương trình bậc hai 
vô nghiệm là 17/36.
13 tháng 4 2023
a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4
CM
17 tháng 4 2018
Đáp án A
Tổng số chấm trên mặt xuất hiện trong hai lần gieo ≥ 11 khi các kết quả là 6 ; 6 , 5 ; 6 , 6 ; 5
Gọi x là xác suất xuất hiện mặt 6 chấm suy ra x 2 là xác suất xuất hiện các mặt còn lại
Ta có 5. x 2 + x = 1 ⇒ x = 2 7 .
Do đó xác suất cần tìm là 2 7 2 + 2 7 . 1 7 + 1 7 . 2 7 = 8 49
Chọn B.
Để tích các số chấm xuất hiện ở năm lần gieo là một số tự nhiên có tận cùng bằng 5 thì phải có ít nhất một lần ra mặt 5 chấm và các mặt khác ra mặt lẻ. Do đó xác suất cần tìm bằng