Trong thí nghiệm Y-âng về ggiao thoa ánh sáng, nguồn sáng phát đồng thời hai bức xạ đơn sắc có bước sóng lần lượt là λ1 = 0,525 μ m và λ2 = 0,675 μ m Khoảng cách giữa hai khe hẹp là a = 1mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là D = 1,2m. Hỏi trên màn quan sát, xét một vùng giao thoa bất kì có bề rộng L = 18mm thì có thể có tối đa bao nhiêu vân tối?
A. 5
B. 4
C. 6
D. 3

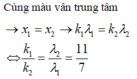






Phương pháp: Giao thoa với ánh sáng đơn sắc
Cách giải:
Khoảng vân của ánh sáng 1 là:
Khoảng vân của ánh sáng 2 là:
Khi trên màn quan sát thấy vân tối thì đó là vân tối trùng nhau của hai ánh sáng 1 và 2.
Xét tỉ số:
Chuyển bài toán thành bài toán giao thoa với ánh sáng có bước sóng I’=0,63.9=5,67mm
Trong miền L = 18mm có số vân tối là:
Vậy nếu ở hai đầu là vân tối thì số vân tối nhiều nhất có thể là 4 vân.
Đáp án B