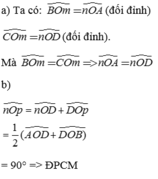Cho hai đường thẳng AB, CD cắt nhau tại O, OM là tia phân giác của COB. Chứng minh rằng tia đối của tia OM là tia phân giác của góc của góc AOD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2018
Ta có:
AB và CD cắt nhau tại O.
=> OA đối OB; OC đối OD.
=> \(\widehat{AOD}\) và \(\widehat{COB}\) là hai góc đối đỉnh.
=> \(\widehat{AOD}=\widehat{COB}\)
Mà: OM là phân giác \(\widehat{AOD}\)
ON là phân giác \(\widehat{COB}\)
=> +) \(\widehat{CON}=\widehat{NOB}=\frac{1}{2}\widehat{COB}\) (1)
+) \(\widehat{AOM}=\widehat{MOD}=\frac{1}{2}\widehat{AOD}\) (2)
Từ (1) và (2) => 
\(\widehat{CON}=\widehat{NOB}=\widehat{AOM}=\widehat{MOD}\)
Mà AB cắt CD tại O
=> CD cắt MN tại O
=> CON đối đỉnh MOD
=> OC đối OD
OM đối ON
Vậy OM đối ON(đpcm)
26 tháng 7 2021
đáp án:
Ta có:
AB và CD cắt nhau tại O.
=> OA đối OB; OC đối OD.
=> ˆAODAOD^ và ˆCOBCOB^ là hai góc đối đỉnh.
=> ˆAOD=ˆCOBAOD^=COB^
Mà: OM là phân giác ˆAODAOD^
ON là phân giác ˆCOBCOB^
=> +) ˆCON=ˆNOB=12ˆCOBCON^=NOB^=12COB^ (1)
+) ˆAOM=ˆMOD=12ˆAODAOM^=MOD^=12AOD^ (2)
Từ (1) và (2) => ˆCON=ˆNOB=ˆAOM=ˆMODCON^=NOB^=AOM^=MOD^
Mà AB cắt CD tại O
=> CD cắt MN tại O
=> CON đối đỉnh MOD
=> OC đối OD
OM đối ON
Vậy OM đối ON(đpcm)
