Cho hình chóp S.ABC có đáy ABC vuông tại C, CH vuông góc với AB tại H, I là trung điểm của đoại HC. Biết SI vuông góc với mặt phẳng đáy,
∠
A
S
B
=
90
0
. Gọi O là trung điểm của đoạn AB, O' là tâm mặt cầu ngoại tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO' và mặt phẳng (ABC) bằng: A.
60
0
B.
30
0
C.
90
0
D.
45
0
...
Đọc tiếp
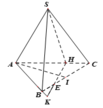
Cho hình chóp S.ABC có đáy ABC vuông tại C, CH vuông góc với AB tại H, I là trung điểm của đoại HC. Biết SI vuông góc với mặt phẳng đáy, ∠ A S B = 90 0 . Gọi O là trung điểm của đoạn AB, O' là tâm mặt cầu ngoại tiếp tứ diện SABI. Góc tạo bởi đường thẳng OO' và mặt phẳng (ABC) bằng:
A. 60 0
B. 30 0
C. 90 0
D. 45 0
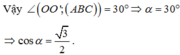
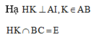
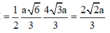
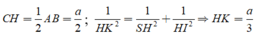
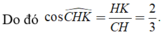
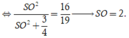
Phương pháp:
- Dựng tâm mặt cầu ngoại tiếp tứ diện.
- Xác định góc giữa OO' và mặt phẳng (ABC), chú ý tìm một đường thẳng song song với OO' suy ra góc.
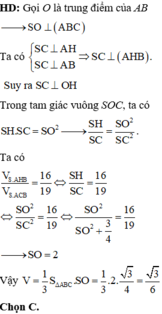
Cách giải:
Gọi J là tâm đường tròn ngoại tiếp tam giác IAB.
Qua J kẻ đường thẳng vuông góc với (IAB), cắt mặt phẳng trung trực của SI tại O' thì O' là tâm mặt cầu ngoại tiếp tứ diện SIAB.
Lại có SI vừa là đường cao vừa là trung tuyến trong tam giác SCH nên tam giác SCH cân tại S