Cho các hàm số f x = x 4 2018 , g x = 2 x 3 - 2018 và h x = 2 x

PT

Pham Trong Bach

12 tháng 2 2019

Cho các hàm số f x = x 4 + 2018 , g x = 2 x 3 - 2018 và h x = 2 x - 1 x + 1 . Trong các hàm số đã cho, có tất cả bao nhiêu hàm số không có khoảng nghịch biến? A. 2 B. 1 C. 0 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

12 tháng 2 2019

Đáp án là A

Đúng(0)

PT

Pham Trong Bach

9 tháng 3 2017

Cho các hàm số f(x) = x4 + 2018, g(x)= 2x3 - 2018 và h ( x ) = 2 x - 1 x + 1 . Trong các hàm số đã cho, có tất cả bao nhiêu hàm số không có khoảng nghịch biến? A. 2 B. 1 C. 0...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

9 tháng 3 2017

Đúng(0)

PT

Pham Trong Bach

22 tháng 7 2018

Cho các hàm số f ( x ) = x 4 + 2018 ; g ( x ) = 2 x 3 - 2018 v à h ( x ) = 2 x - 1 x + 1 . Trong các hàm số đã cho, có tất cả bao nhiêu hàm số không có khoảng nghịch biến? A. 2 B. 1 C. 0 D....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

22 tháng 7 2018

Đáp án là A

nên hàm số có khoảng đồng biến và nghịch biến.

nên hàm số luôn đồng biến trên R.

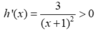nên hàm số luôn đồng biến trên từng khoảng xác định.

Vậy có 2 hàm số không có khoảng nghịch biến.

Đúng(0)

PT

Pham Trong Bach

16 tháng 11 2019

Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A. 1 ; + ∞ B. 0 ; 3 C. - ∞ ; 3 D. 3 ; + ∞ ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

16 tháng 11 2019

Đáp án D

Ta có Đáp án D

Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018

= –x(3–x)g(1–x)

Suy ra 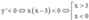(vì g(1–x) < 0, ∀ x ∈ R )

Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞

Đúng(0)

PT

Pham Trong Bach

22 tháng 3 2019

Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

22 tháng 3 2019

Đúng(0)

PT

Pham Trong Bach

23 tháng 10 2019

Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018 với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019 nghịch biến trên khoảng nào dưới đây? A . ( 1 ; + ∞ ) . B ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

23 tháng 10 2019

Đúng(0)

PT

Pham Trong Bach

13 tháng 1 2019

Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào? ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

13 tháng 1 2019

Đúng(0)

PT

Pham Trong Bach

19 tháng 7 2017

Cho hàm số f(x)= x(x-1)(x-2) (x-3)... (x-2018).

Tính f'(1)

A. -2017!

B. 0

C. 2017!

D. 2018

#Toán lớp 12

1

CM

Cao Minh Tâm

19 tháng 7 2017

Đúng(0)

PT

Pham Trong Bach

24 tháng 12 2019

Cho hàm số y=f(x)>0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)=1+2018 ∫ 0 x f ( t ) dt ; g ( x ) = f 2 ( x ) . Tính ∫ 0 1 ( g ( x ) dx ? A. 1011/2. B. 1009/2. C. 2019/2. ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

24 tháng 12 2019

Đúng(0)

PT

Pham Trong Bach

27 tháng 2 2018

Cho hàm số y=f(x)=x(x+1)(x+2)(x+3)...(x+2018)(x+2019). Tínhf’(0). A. 0. B. 2019 1 + 2019 2 C. P 2019 D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

27 tháng 2 2018

Đúng(0)

M

moon

10 tháng 1 2020 - olm

Cho f ( x ) = \(x^{2020}-x^{2019}+x^{2018}-...+x^2-x+1\)

và G ( x ) = \(1-x+x^2-...+x^{2018}-x^{2019}+x^{2020}\)

Tính giá trị của đa thức h ( x ) tại x = 2020 biết :

h ( x ) = [ f ( x ) + G ( x ) ] * [ G ( x ) - f ( x ) ]

#Toán lớp 7

1

MT

►♣Mînh♣◄ ♡๖ۣۜŦεαм♡❤Ɠ长♡ღ

20 tháng 5 2020

Tính [G_(x) - f_(x)] = ( \(1-x^2+.....+x^{2020}\)) - (\(x^{2020}-x^{2019}+....-x+1\))

= (\(x^{2020}-x^{2019}+....-x+1\)) - (\(x^{2020}-x^{2019}+....-x+1\))

= 0

=> h_(x) = [G_(x) - f_(x) ] * [G_(x) + f_(x) ]

= 0 * [G_(x) + f_(x) ]

= 0

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP