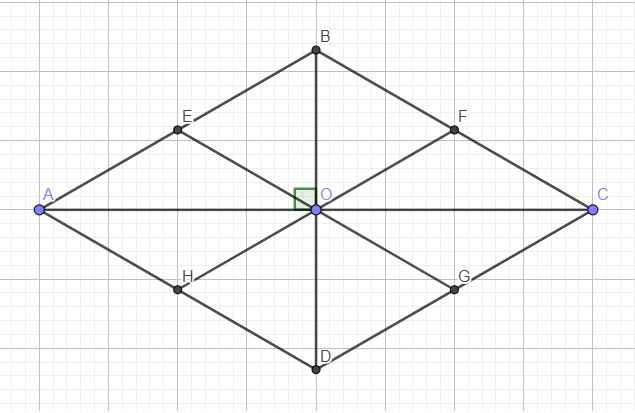
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H theo thứtựlà giao điểm của AE, AF với đường chéo BD. Chứng minh rằng tứgiác AGCH là hình thoi.
*Gợi ý:
+Gọi O là giao điểm của AC và BD
+ Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD ta có:
+Xét tam giác ABE và tam giác ADFAB =.... ; 𝐵̂=⋯; BE =...
Suy ra: ∆ABE =.... ( .........)
Suy ra 𝐵𝐴𝐸̂=⋯( 2 góc tương ứng)
Mà AC là phân giác của góc 𝐵𝐴𝐷̂=> 𝐸𝐴𝐶̂=⋯(1)
Do đó AO là phân giác của góc HAG
Xét tam giác AGH có AO là đường phân giác, là đường cao
=> ∆AGH là tam giác cân tại A
=> HO =.... (2)
Vì ABCD là hình thoi nên AO =.... (3)
Từ(1), (2), (3) suy ra AGCH là hình thoi.