Kết quả (b,c) của việc gieo con súc sắc cân đối và đồng chất hai lần (trong đó b là số chấm xuất hiện trong lần gieo đầu, c là số chấm xuất hiện ở lần gieo thứ hai) được thay vào phương trình x 2 + b x + c x + 1 = 0 * . Xác suất để phương trình (*) vô nghiệm là :
A. 17 36 .
B. 1 2 .
C. 1 6 .
D. 19 36 .

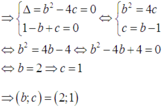
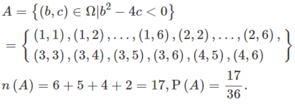
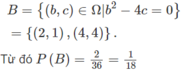
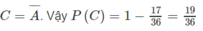



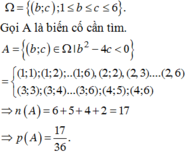
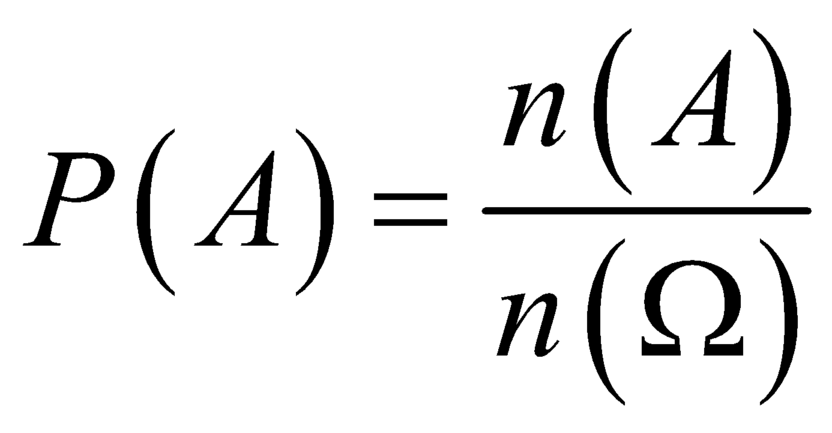 , với
, với
Đáp án B
Xác suất của biến cố A là n A n Ω trong đó là n A số khả năng mà biến cố A có thể xảy ra, n Ω là tất cả các khả năng có thể xảy ra.
x 2 + b x + c x + 1 = 0 *
Để phương trình (*) vô nghiệm thì phương trình x 2 + b x + c = 0 * * có 2 trường hợp xảy ra:
TH1: PT (**) có 1 nghiệm x= -1
⇒ Δ = b 2 − 4 c = 0 1 − b + c = 0 ⇔ b 2 = 4 c c = b − 1 ⇔ b 2 = 4 b − 4 ⇔ b 2 − 4 b + 4 = 0 ⇔ b = 2 ⇒ c = 1
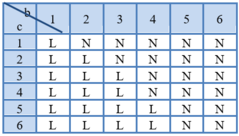
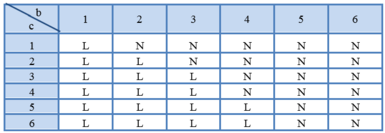
TH2: PT (**) vô nghiệm ⇔ Δ = b 2 − 4 c < 0 ⇒ b 2 < 4 c ⇔ b < 2 c
Vì c là số chấm xuất hiện ở lần gieo thứ 2 nên . c ≤ 6 ⇒ b ≤ 2 6 ≈ 4,9
Mà b là số chấm xuất hiện ở lần giao đầu nên b ∈ 1 ; 2 ; 3 ; 4
Với b=1 ta có: c > 1 4 ⇒ c ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ⇒ có 6 cách chọn c.
Với b=2 ta có: c > 1 ⇒ c ∈ 2 ; 3 ; 4 ; 5 ; 6 ⇒ có 5 cách chọn c.
Với b=3 ta có: c > 9 4 ⇒ c ∈ 3 ; 4 ; 5 ; 6 ⇒ có 4 cách chọn c.
Với b=4 ta có: c > 4 ⇒ c ∈ 5 ; 6 ⇒ có 2 cách chọn c.
Do đó có 6 + 5 + 4 + 2 = 17 cách chọn để phương trình (**) vô nghiệm.
Gieo con súc sắc 2 lần nên số phần tử của không gian mẫu n Ω = 6.6 = 36
Vậy xác suất đề phương trình (*) vô nghiệm là 1 + 17 36 = 1 2 .