Cho hình chóp S.ABC có thể tích bằng a 3 3 3 , đáy là tam giác đều cạnh a 3 . Tính chiều cao h của hình chóp đã cho.
A. h = 4 a 3 .
B. h = a 4 .
C. h = 4 a .
D. h = 3 a 4 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình chóp S.ABC có đáy ABC là tam giác đều cạnh ![]()
Thể tích khối chóp 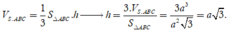
Chọn A.

Đáp án A
Diện tích đáy là:
S d = B A . B C 2 = a 2 ⇒ h = 3 V S = 3 a 2

Đáp án D
Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:

Đáp án A.
Ta có m .3 x 2 − 7 x + 12 − 1 + 3 2 x − x 2 = 9.3 10 − 5 x + m ⇔ m . 3 x 2 − 7 x + 12 − 1 = 3 12 − 5 x − 3 2 x − x 2 .
⇔ m . 3 x 2 − 7 x + 12 − 1 = 3 2 x − x 2 3 x 2 − 7 x + 12 − 1 ⇔ 3 x 2 − 7 x + 12 − 1 3 2 x − x 2 − m = 0
⇔ 3 x 2 − 7 x + 12 = 1 3 2 x − x 2 − m = 0 ⇔ x 2 − 7 x + 12 = 0 2 x − x 2 = log 3 m ⇔ x = 4 ; x = 3 2 x − x 2 = log 3 m *
Để phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi
(*) có nghiệm duy nhất khác 4 ; 3 .
(*) có hai ngiệm phân biệt, 1 nghiệm bằng 4, nghiệm còn lại khác 3.
(*) có hai nghiệm phân biệt, 1 nghiệm bằng 3, nghiệm còn lại khác 4.
Vậy có 3 giá trị m cần tìm.