Khi thiết kế vỏ lon người ta đặt mục tiêu sao cho chi phí làm ít nhất. Muốn thể tích lon là V mà diện tích toàn phần nhỏ nhất thì bán kính đáy vỏ lon R bằng?
A. V 2 π 3
B. V π 3
C. 3 π 2 V 3
D. 3 V 2 π 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có V t = V = l . π R 2 ⇒ l = V π R 2
S t = l .2 π R + 2 π R 2 ⇒ S t = V π R 2 π R + 2 π R 2 = 2 ( π R 2 + V R )
S t = 2 ( π R 2 + V 2 R + V 2 R ) ≥ 2.3 π R 2 . V 2 R . V 2 R 3 = 6 π V 2 4 3
Dấu “=” xảy ra khi và chỉ khi π R 2 = V 2 R ⇔ R = V 2 π 3

Chọn đáp án A.
Gọi r, h lần lượt là bán kính đáy và chiều cao của lon sữa bò cần thiết kế.

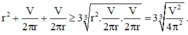
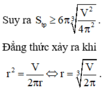

Đáp án: 28,1
Giải thích các bước giải:
a) Đường kính đáy của hình nón đó là:
d = 2 . r = 2 . 2 = 4
Vì chiều cao của hình nón đó bằng đường kính đáy của hình nón đó nên chiều cao h của hình nón đó là: h = 4 (cm)
Ta có: l² = r² + h² (theo định lý Py - ta - go)
⇒ l = √(r² + h²) = √(2² + 4²) = √(4 + 16) = √20 (cm)
Diện tích xung quanh của hình nón đó là: Sxq = π . r . l = π . 2 . √20 ≈ 28,1(cm²)
Vậy diện tích xung quanh của hình nón đó là ≈ 28,1