Cho a,b,c là các số thực sao cho phương trình z 3 + a z 2 + b z + c = 0 có ba nghiệm phức lần lượt là z 1 = ω + 3 i ; z 2 = ω + 9 i ; z 3 = 2 ω - 4 , trong đó ω là một số phức nào đó. Tính giá trị của P=|a+b+c|.
A. P=36
B. P=136
C. P=208
D. P=84
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Nếu $z_1,z_2,z_3$ là 3 nghiệm phức của pt \(2x^3-3x-2=0\) thì theo định lý Vi-et ta có:
\(\left\{\begin{matrix} z_1+z_2+z_3=0\\ z_1z_2z_3=1\end{matrix}\right.\)
Kết hợp hệ phương trình trên với hằng đẳng thức:
\(z_1^3+z_2^3+z_3^3=(z_1+z_2)^3-3z_1z_2(z_1+z_2)+z_3^3\)
\(=(-z_3)^3-3z_1z_2(-z_3)+z_3^3=3z_1z_2z_3=3\)
Đáp án B

Chọn D.
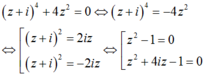
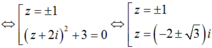
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.

Ta có 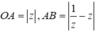
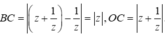
Vì OABC là một hình bình hành nên
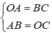
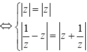
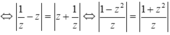
![]()
Đặt ![]() vậy điều kiện trở thành:
vậy điều kiện trở thành:
![]()
![]()
![]()
![]()
![]()
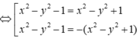
![]()
Khi đó
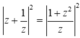
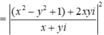
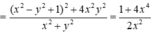
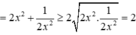
Dấu bằng đạt tại 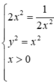
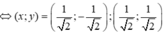
Chọn đáp án B.
Đáp án B