Cho hàm số y = 4 3 x 3 + 4 x 2 = m x + 10 (1) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của tham số thực m lớn hơn -10 để hàm số (1) đồng biến trên khoảng - ∞ ; 0
A. 5
B. 4
C. 6
D. 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
16 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
CM
14 tháng 11 2017
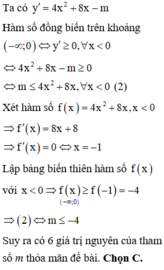
+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.
HP
22 tháng 3 2021
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
CM
1 tháng 12 2018
Chọn D
.
: 
Hàm số đồng biến trên 
thỏa mãn.
:
.
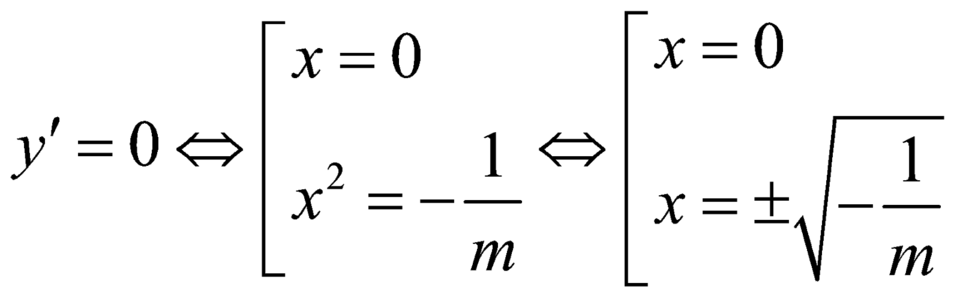BBT :
Dựa vào BBT, hàm số đồng biến trên khoảng
.
So với điều kiện 
.
Mặt khác, theo giả thiết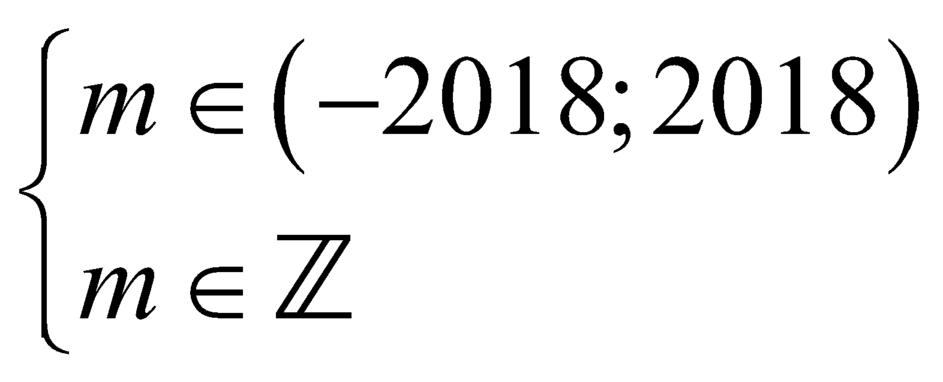 
suy ra có 
giá trị nguyên của 
thỏa mãn yêu cầu bài toán.
AM
14 tháng 2 2022
Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)
\(\Leftrightarrow mx-2x+2m-3\ge0\)
\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)
\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)
\(\Rightarrow1\le m\le\dfrac{11}{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2022
- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)