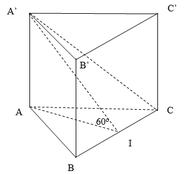
Cho hình lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 o , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A'B'C' là
A. 2 3
B. - 2
C. 3 3
D. - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
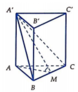
Gọi M là trung điểm BC. Ta có A ' M A ^ = 60 0
AM là trung tuyến trong tam giác đều cạnh a nên AM = a 3 2
![]()
![]()
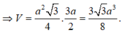


a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)

Đáp án A
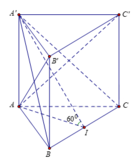
Gọi I là trung điểm của BC. Ta có:
A I = a 3 2 ⇒ A ' A = A I tan 60 ° = 3 a 2
S B C C ' B ' = 3 a 2 a = 3 a 2 2
Thể tích của khối chóp A B C C ' B ' là:
V = 1 3 A I . S B C C ' B ' = 1 3 . a 3 2 . 3 a 2 4 = a 3 3 4

Đáp án A
Ta có:
A I = 2 a 2 − a 2 = a 3 ; A A ' = A I tan 60 ° = a 3 . 3 = 3 a
Thể tích lăng trụ là:
V = A A ' . S A B C = 3 a . 1 2 2 a 2 sin 60 ° = 3 3 a 3
Chọn C