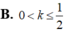
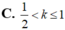
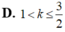
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có:
log a x > log b x > 0 > log c x ⇔ 1 log x a > 1 log x b > 0 log x c < 0 ⇔ log x b > log x c > 0 c < 1 ⇔ b > a > 1 > c .
Đáp án A
Ta có: F x = ∫ e x ln a x + + 1 x d x = ∫ e x ln a x d x + ∫ e x x d x = I 1 + I 2
Tính I 2 = ∫ e x d x x ,đặt u = e x d v = 1 x d x ⇒ d u = e x d x v = ln x ⇒ I 2 = e x ln x - ∫ e x ln x d x
Do đó F x = e x ln x + ∫ e x ln a x - ln x d x = e x ln x + ∫ e x ln a d x = e x ln x + ln a + C = e x ln a x + C
Lại có : F 1 a = e 1 a ln 1 + C = 0 ⇒ C = 0 ; F 2018 = e 2018 ln 2018 a e 2018
Do đó ln 2018 a = 1 ⇒ a = e 2018 .
.
Chọn C