Trong không gian với hệ tọa độ Oxy, cho đường thẳng d: x - 1 1 = y - 2 1 = z - 1 2 ,A(2;1;4). Gọi H(a,b,c) là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính T = a 3 + b 3 + c 3
A. T=8
B. T=62
C. T=13
D. T= 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
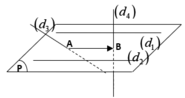
Ta có d1 song song d2, phương trình mặt phẳng chứa hai đường thẳng d1, d2 là
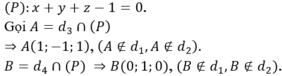
Mà ![]() cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.

Đáp án D
Phương pháp:
Đường thẳng d: x - x 0 a = y - y 0 b = z - z 0 c có 1 VTCP là a → = a ; b ; c
Cách giải: Đường thẳng d có 1 VTCP là a → = 3 ; - 2 ; 1

Đáp án C
Gọi B 2 + t ; - 1 - t ; 1 + t A B ¯ = 1 + t ; - t ; t - 2 . Cho A B ¯ . u d ¯ = 0 ⇔ t + 1 - 4 t - 2 t + 4 = 0 ⇔ t = 1 ⇒ A B ¯ = 2 ; - 1 ; - 1
Khi đó d : x - 1 2 = y + 1 - 1 = z - 3 - 1 .