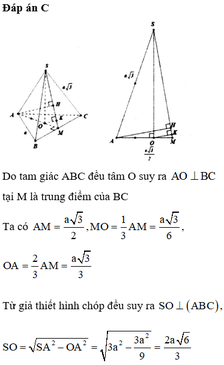
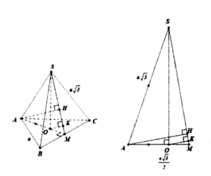
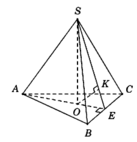
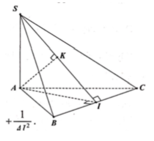
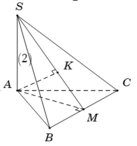
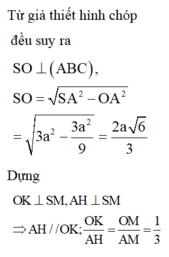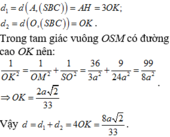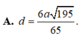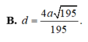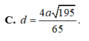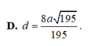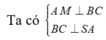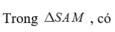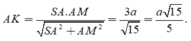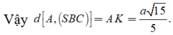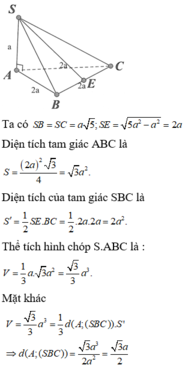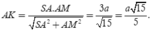Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3 . Gọi O là tâm đáy ABC, d 1 là khoảng cách từ A đến mặt phẳng (SBC) và d 2 là khoảng cách từ O đến mặt phẳng (SBC). Tính d = d 1 + d 2
A. d= 2a 2 /11
B. d= 2a 2 /33
C. d= 8a 2 /33
D. d= 8a 2 /11