Tìm tất cả các giá trị của m để hàm số y = 1 3 x 3 − m x 2 + m 2 − m + 1 đạt cực đại tại x=1
A. m = -1
B.m = 1
C.m = 2
D. m = -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
(không tồn tại m).
CM
4 tháng 9 2019
Đáp án C
y ' = x 2 − 2 m x + m 2 − m + 1 y ' ' = 2 x − 2 m ⇒ y ' ( 1 ) = m 2 − 3 m + 2 = 0 y ' ' ( 1 ) = 2 − 2 m < 0 ⇒ m = 1 ( l ) m = 2 ( n ) m > 1 ⇒ m = 2
(Cách khác: Hs kiểm tra trên MTBT vẫn đc m =2)
CM
3 tháng 10 2018
Đáp án A.
Tập xác định D = R.
y' = x2 – 2(m + 1)x + m2 – 3, y’’ = 2x – 2(m + 1).
Hàm số đạt cực trị tại x = -1
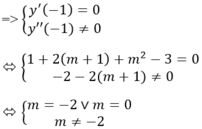
Vậy m = 0 thì hàm số đạt cực trị tại x = -1
Đáp án C
Ta có
y ' = x 2 − 2 m x + m 2 − m + 1 y ' ' = 2 x − 2 m ⇒ y ' ( 1 ) = m 2 − 3 m + 2 = 0 y ' ' ( 1 ) = 2 − 2 m < 0 ⇒ m = 1 ( l ) m = 2 ( n ) m > 1 ⇒ m = 2
(Cách khác: Hs kiểm tra trên MTBT vẫn đc m =2)