Biết 2 x + 2 - x = 4 . Tính M = 4 x + 4 - x + 2
A. M = 12
B. M = 3
C. M = 18
D. M = 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
4 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
29 tháng 3 2020
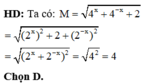
Phần a tính rất đơn giản nên bạn tự làm nha
b)\(\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...........+\frac{1}{x.\left(x+1\right)}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{2.3}+\frac{1}{3.4}+.............+\frac{1}{x.\left(x+1\right)}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...........+\frac{1}{x}-\frac{1}{x+1}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{x+1}=\frac{2}{5}\)
\(\Rightarrow\frac{x+1}{2.\left(x+1\right)}-\frac{2}{2.\left(x+1\right)}=\frac{2}{5}\)
\(\Rightarrow\frac{x-1}{2.\left(x+1\right)}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{2}.\frac{x-1}{x+1}=\frac{2}{5}\)
\(\Rightarrow\frac{x-1}{x+1}=\frac{2}{5}:\frac{1}{2}\)
\(\Rightarrow\frac{x-1}{x+1}=\frac{2}{5}.2\)
\(\Rightarrow\frac{x-1}{x+1}=\frac{4}{5}\Rightarrow x\in\varnothing\)(vì x+1 và x-1 cách nhau 2 đơn vị; mà 4;5 cách nhau 1 đơn vị)
Vậy \(x\in\varnothing\)
Chúc bn học tốt
9 tháng 2 2019
a) Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|x-1\right|+\left|x+3\right|=\left|1-x\right|+\left|x+3\right|\ge\left|1-x+x+3\right|=4\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}1-x\ge0\\x+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow-3\le x\le1\)
Vậy,..................................................................................................................................
17 tháng 8 2022
a: =>(x-6)(x+2)=0
=>x=6 hoặc x=-2
b: \(\Leftrightarrow25x^2+10x+1-25x^2+9=30\)
=>10x=20
hay x=2
c: =>x3-1-x3+4x=5
=>4x=6
hay x=3/2
24 tháng 3 2022
a/Ta có: M(x)+N(x) = (2x5 - 4x3 + 2x2 + 10x - 1) + (-2x5 + 2x4 + 4x3 + x2 + x - 10)
= 2x5 - 2x5 - 4x3 + 4x3 + 2x4 + 2x2 + x2 + 10x + x -1 - 10
= 2x4 + 3x2 + 11x - 11
b/ Ta có: A(x) = N(x)-M(x) = (-2x5 + 2x4 + 4x3 + x2 + x - 10) - (2x5 - 4x3 + 2x2 + 10x - 1)
= -2x5 - 2x5 + 2x4 + 4x3 + 4x3 + x2 - 2x2 + x - 10x -10 + 1
= -2x5 + 2x4 + 8x3 - x2 - 9x -9
JS
22 tháng 3 2020
a) \(x+1+x+2+x+3+x+\frac{1}{4}+x+100=7450\)
\(\Leftrightarrow5x+\frac{425}{4}=7540\)
\(\Leftrightarrow x=\frac{5947}{4}\)
Vậy...
b) \(M=3+3^2+3^3+3^4+...+3^{99}+3^{100}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{99}+3^{100}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{99}\left(1+3\right)\)
\(=4\left(3+3^3+...+3^{99}\right)⋮4\)
Ta lại có:
\(M=3+3^2+3^3+3^4+...+3^{99}+3^{100}\)
\(=\left(3+3^3\right)+\left(3^3+3^4\right)+...+\left(3^{99}+3^{100}\right)\)
\(=\left(3+3^2\right)+3\left(3+3^2\right)+...+3^{98}\left(3+3^2\right)\)
\(=12\left(1+3+...+3^{98}\right)⋮12\)
Chúc bạn học tốt@@
19 tháng 2 2021
a) Ta có: \(M=\left(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\right)\cdot\dfrac{x+3\sqrt{x}}{7-\sqrt{x}}\)
\(=\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-\left(x-2\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)}\cdot\dfrac{1}{-\left(\sqrt{x}-7\right)}\)
\(=\dfrac{\sqrt{x}-7}{\sqrt{x}-2}\cdot\dfrac{-1}{\sqrt{x}-7}\)
\(=\dfrac{-1}{\sqrt{x}-2}\)(1)
b) Ta có: \(x^2-4x=0\)
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
Thay x=0 vào biểu thức (1), ta được:
\(M=\dfrac{-1}{\sqrt{0}-2}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Vậy: Khi \(x^2-4x=0\) thì \(M=\dfrac{1}{2}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) \((3{x^6}):(0,5{x^4}) = (3:0,5).({x^6}:{x^4}) = 6.{x^{6 - 4}} = 6{x^2}\);
b) \(( - 12{x^{m + 2}}):(4{x^{n + 2}}) = ( - 12:4).({x^{m + 2}}:{x^{n + 2}}) = - 3.{x^{m + 2 - n - 2}} = - 3.{x^{m - n}}\)(m, n \(\in\) N, m ≥ n).