Cho x, y là các số thực thỏa mãn l o g 4 ( x + y ) + l o g 4 ( x - y ) ≥ 1 . Biết giá trị nhỏ nhất của biển thức P=2x-y là a b ( 1 < a , b ∈ Z ). Giá trị a 2 + b 2
A. a 2 + b 2 =18 x
B. a 2 + b 2 =8
C. a 2 + b 2 =13
D. a 2 + b 2 =20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
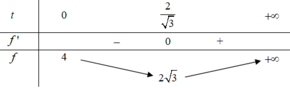
Phương pháp
Biến đổi giả thiết để tìm mối liên hệ của x theo y. Thay vào biểu thức P rồi sử dụng phương pháp hàm số để tìm giá trị nhỏ nhất của P.
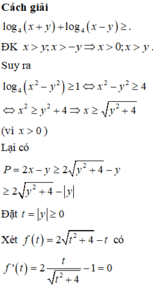
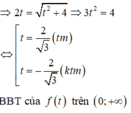


Ta sẽ chứng minh \(P_{min}=1\)
TH1: \(xyz=0\)
\(\Rightarrow x^2y^2z^2=0\Rightarrow x^4+y^4+z^4=1\)
\(P=x^2+y^2+z^2\ge\sqrt{x^4+y^4+z^4}=1\)
TH2: \(xyz\ne0\) , từ điều kiện, tồn tại 1 tam giác nhọn ABC sao cho \(\left\{{}\begin{matrix}x^2=cosA\\y^2=cosB\\z^2=cosC\end{matrix}\right.\)
\(P=cosA+cosB+cosC-\sqrt{2cosA.cosB.cosC}\)
Ta sẽ chứng minh \(cosA+cosB+cosC-\sqrt{2cosA.cosB.cosC}\ge1\)
\(\Leftrightarrow4sin\dfrac{A}{2}sin\dfrac{B}{2}sin\dfrac{C}{2}\ge\sqrt{2cosA.cosB.cosC}\)
\(\Leftrightarrow8sin^2\dfrac{A}{2}sin^2\dfrac{B}{2}sin^2\dfrac{C}{2}\ge cosA.cosB.cosC\)
\(\Leftrightarrow\dfrac{8sin^2\dfrac{A}{2}sin^2\dfrac{B}{2}sin^2\dfrac{C}{2}}{8sin\dfrac{A}{2}sin\dfrac{B}{2}sin\dfrac{C}{2}cos\dfrac{A}{2}cos\dfrac{B}{2}cos\dfrac{C}{2}}\ge cotA.cotB.cotC\)
\(\Leftrightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\ge cotA.cotB.cotC\)
\(\Leftrightarrow tanA.tanB.tanC\ge cot\dfrac{A}{2}cot\dfrac{B}{2}cot\dfrac{C}{2}\)
\(\Leftrightarrow tanA+tanB+tanC\ge cot\dfrac{A}{2}+cot\dfrac{B}{2}+cot\dfrac{C}{2}\)
Ta có:
\(tanA+tanB=\dfrac{sin\left(A+B\right)}{cosA.cosB}=\dfrac{2sinC}{cos\left(A-B\right)-cosC}\ge\dfrac{2sinC}{1-cosC}=\dfrac{2sin\dfrac{C}{2}cos\dfrac{C}{2}}{2sin^2\dfrac{C}{2}}=cot\dfrac{C}{2}\)
Tương tự: \(tanA+tanC\ge cot\dfrac{B}{2}\) ; \(tanB+tanC\ge cot\dfrac{A}{2}\)
Cộng vế với vế ta có đpcm
Vậy \(P_{min}=1\) khi \(\left(x^2;y^2;z^2\right)=\left(1;0;0\right)\) và các hoán vị hoặc \(\left(x^2;y^2;z^2\right)=\left(\dfrac{1}{2};\dfrac{1}{2};\dfrac{1}{2}\right)\)

Bạn kiểm tra lại đề bài, với biểu thức thế này thì không thể tìm được điểm rơi (nó là nghiệm của 1 pt bậc 4 hệ số rất xấu ko thể giải được)

Chọn đáp án B
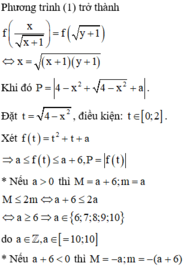
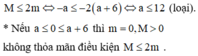
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

ĐK: x khác 0
Từ\(2x^2+\frac{y^2}{4}+\frac{1}{x^2}=4\)
\(\Rightarrow x^2+2+\frac{1}{x^2}+x^2+xy+\frac{y^2}{4}=6+xy\)
\(\Leftrightarrow\left(x+\frac{1}{x}\right)^2+\left(x+\frac{y}{2}\right)^2=6+xy\)
Do VT > 0\(\Rightarrow6+xy\ge0\Rightarrow xy\ge6\)
Có A = 2016 + xy > 2016 + 6 = 2022
tth : Viết nhầm :V
Đoạn cuối \(6+xy\ge0\Rightarrow xy\ge-6\)
Có A = 2016 + xy > 2016 - 6 = 2010 !!!
Được rồi chứ gì -.-

\(P=\left(x^2+y^2\right)^2-2x^2y^2-4xy+3=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2-4xy+3\)
\(=\left(16-2xy\right)^2-2x^2y^2-4xy+3=2x^2y^2-68xy+259\)
\(4=x+y\ge2\sqrt[]{xy}\Rightarrow0\le xy\le4\)
Đặt \(xy=a\Rightarrow0\le a\le4\)
\(P=2a^2-68a+259=259-2a\left(34-a\right)\le259\)
\(P_{max}=259\) khi \(a=0\) hay \(\left(x;y\right)=\left(4;0\right);\left(0;4\right)\)
\(P=\left(2a^2-68a+240\right)+19=2\left(4-a\right)\left(30-a\right)+19\ge19\)
\(P_{min}=19\) khi \(a=4\) hay \(x=y=2\)

\(y\ge1+xy\Rightarrow1\ge\dfrac{1}{y}+x\ge2\sqrt{\dfrac{x}{y}}\Rightarrow\dfrac{x}{y}\le4\Rightarrow\dfrac{y}{x}\ge4\)
\(G=\dfrac{x}{y}+\dfrac{y}{x}=\left(\dfrac{x}{y}+\dfrac{y}{16x}\right)+\dfrac{15}{16}.\dfrac{y}{x}\ge2\sqrt{\dfrac{xy}{16xy}}+\dfrac{15}{16}.4=\dfrac{17}{4}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{2};2\right)\)