Thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường y = 1 x − 3 , y = 0 , x = 0 , x = 2 quay một vòng quanh trục Ox là (theo đơn vị thể tích)
A. 2 π
B. 2 3 π
C. 4 3 π
D. 1 3 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(V=\pi\int\limits^4_0\left(\dfrac{e^x}{4}\right)^2dx=\pi\int\limits^4_0\dfrac{e^{2x}}{16}dx=\dfrac{\pi}{32}.e^{2x}|^4_0=\dfrac{\pi}{32}\left(e^8-1\right)\)

Phương pháp:
Thể tích vật thể được sinh ra khi
cho hình phẳng giới hạn bởi các đường
![]()
![]()
Cách giải:
Thể tích cần tìm là
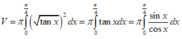
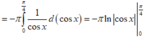
![]()
Chọn A.

Đáp án B
Phương pháp
Sử dụng công thức ứng dụng tích phân để tính thể tích vật tròn xoay
Cách giải
V = π ∫ 1 4 d x x 2 = π − 1 x 1 4 = π − 1 4 + 1 = 3 π 4

Đáp án B.
Thể tích vật thể cần tính là:
V = π ∫ 1 a 1 x 2 d x = π ∫ 1 a d x x 2 = − π x a 1 = π − π a .
Đáp án B.
Thể tích khối tròn xoay là:
V o x = π ∫ 0 2 1 x − 3 2 d x = − π x − 3 0 2 = π − π 3 = 2 π 3