Cho hình chóp tứ giác đều S.ABCD, cạnh đáy bằng a, đường cao SO bằng h. Khoảng cách giữa SB và AD là
A. 3 a h 4 h 2 + a 2
B. a h 4 h 2 + a 2
C. 2 a h 4 h 2 + a 2
D. 4 a h 4 h 2 + a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do S.ABCD là chóp tứ giác đều \(\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\)
Mà \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow AC\perp\left(SBD\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b. Qua B kẻ đường thẳng song song AC cắt DC kéo dài tại E
\(\Rightarrow AC||\left(SBE\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SBE\right)\right)=d\left(H;\left(SBE\right)\right)\)
\(\left\{{}\begin{matrix}AC\perp\left(SBD\right)\\AC||BE\end{matrix}\right.\) \(\Rightarrow BE\perp\left(SBD\right)\)
Trong tam giác vuông SBH, từ H kẻ \(HK\perp SB\Rightarrow HK\perp\left(SBE\right)\)
\(\Rightarrow HK=d\left(H;SBE\right)\)
\(BD=a\sqrt{2}\Rightarrow BH=\dfrac{BD}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{3}}{2}\)
ÁP dụng hệ thức lượng:
\(HK.SB=SH.BH\Rightarrow HK=\dfrac{SH.BH}{SB}=\dfrac{a\sqrt{30}}{10}\)

Đáp án C
Gọi O là giao điểm của AC và BD. Ta có AC vuông góc với mặt phẳng (SBD) tại O. Kẻ OH vuông góc với SB, thì OH là khoảng cách cần tìm. Tam giác SOB vuông cân tại O, nên O H = S B 2 = a 2 .

Đáp án B
Hướng dẫn giải:
+)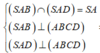
![]()
![]()
+) ![]()
![]()
+) Ta có A B ⊥ B C , kẻ A P ⊥ S B ( P ∈ S B )
d(A;(SBC)) = AP ⇒ d(AD;SB) = AP
+) 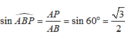
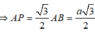
![]()

\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)
Đáp án C.
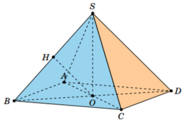
Gọi O chân đường cao hạ từ S xuống mặt đáy ⇒ A C ∩ B D = O .
Dựng O H ⊥ S N (H thuộc SN). Gọi M, N lần lượt là trung điểm của AD và BC. Trong (SMN), kẻ M I // O H (I thuộc SN).
Em có: AD//BC⇒d S B , A D = d A D , S B C = d M , S B C .
Em lại có: S M N ⊥ S B C ⇒ OH ⊥ S B C
Do O H // M I nên MI⊥SBC⇒d M , S B C = M I = 2 O H .
Tam giác SON vuông tại O, đường cao OH nên ta có
1 O H 2 = 1 S O 2 + 1 O N 2 ⇒ O H = a h 4 h 2 + a 2 ⇒ M I = 2 a h 4 h 2 + a 2