Cho hình chóp S.ABC. Gọi M là một điểm thuộc miền trong của tam giác ABC. Từ M kẻ các đường thẳng song song với SA, SB, SC lần lượt cắt các mặt bên SBC, SCA, SAB tại A1, B1, C1. Gọi G1 là trọng tâm ta...

K

Khách

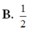
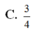
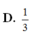
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

10 tháng 6 2018

Cho hình chóp S.ABC. Gọi M là một điểm thuộc miền trong của tam giác ABC. Từ M kẻ các đường thẳng song song với SA, SB, SC lần lượt cắt các mặt bên SBC, SCA, SAB tại A1, B1, C1. Gọi G1 là trọng tâm tam giác A1B1C1. Tỉ số S G 1 S M bằng ...

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 6 2018

Những câu hỏi liên quan

PT

Pham Trong Bach

4 tháng 1 2017

Cho hình chóp S.ABC. Gọi M là một điểm thuộc miền trong của tam giác ABC. Từ M kẻ các đường thẳng song song với SA, SB, SC lần lượt cắt các mặt bên SBC, SCA, SAB tại A 1 , B 1 , C 1 . Gọi G 1 là trọng tâm tam giác A 1 B 1 C 1 . Tỉ số S G 1 S M bằng A. 2 3 B. ...

1

CM

Cao Minh Tâm

4 tháng 1 2017

Chọn A

PT

Pham Trong Bach

25 tháng 3 2019

Cho hình chóp S.ABC. Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng (SBC), (SCA), (SAB) theo thứ tự tại các điểm A’, B’, C’. Tính tổng tỉ số T = O A ' S A + O A ' S B + O C ' S C ...

#Toán lớp 12

1

CM

Cao Minh Tâm

25 tháng 3 2019

PT

Pham Trong Bach

21 tháng 5 2019

Cho hình chóp S . A B C . Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng S B C , S C A , S A B theo thứ tự tại các điểm A’ , B’ , C’ . Tính tổng tỉ số T = O A ' S A + O B ' S ...

1

CM

Cao Minh Tâm

21 tháng 5 2019

Đáp án C

Gọi M,N,P lần lượt là giao điểm của OA, OB, OC với cạnh BC, CA, AB.

Vì O B ' / / S A ⇒ O A ' S A = O M A M (Định lí Thalet).

Tương tự, ta có O B ' S B = O N B N ' ; O C ' S C = O P P C ⇒ T = O M A M + O N B N + O P P C .

Với O là trọng tâm của tam giác ABC ⇒ M , N , P lần lượt là trung điểm của BC, CA, AB

⇒ O M A M = O N B N = O P C P = 1 3 . Vậy tổng tỉ số T = O A ' S A + O B ' S B + O C ' S C = 1.

Chú ý: Bản chất bài toán là yêu cầu chứng minh O M A M + O N B N + O P P C = 1. Tuy nhiên với tinh thần trắc nghiệm ta sẽ chuẩn hóa với O là trọng tâm tam giác ABC.

PT

Pham Trong Bach

14 tháng 10 2017

Cho hình chóp S.ABC có SA=SB=CA=CB=AB=a, S C = a 3 2 , G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng A. 90 0 C B. 45 0 C C. 30 0 C ...

1

CM

Cao Minh Tâm

14 tháng 10 2017

Chọn đáp án D

Ta có

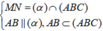
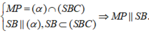
Khi đó

Gọi I là trung điểm của AB.

Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.

Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a

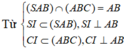
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều

Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0

PT

Pham Trong Bach

8 tháng 3 2017

Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AC=a 2 , SA ⊥ (ABC), SA=a. Gọi G là trọng tâm tam giác SBC, mặt phẳng ( α ) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN. ...

#Toán lớp 12

1

CM

Cao Minh Tâm

8 tháng 3 2017

PT

Pham Trong Bach

7 tháng 12 2018

Cho hình chóp S. ABCD. Gọi A 1 là trung điểm của cạnh SA và A 2 là trung điểm của đoạn A A 1 . Gọi (α) và (β) là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua A 1 , A 2 . Mặt phẳng (α) cắt các cạnh SB, SC, SD lần lượt tại B 1 , C 1 , D 1 . Mặt phẳng (β)...

#Toán lớp 11

1

CM

Cao Minh Tâm

7 tháng 12 2018

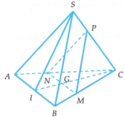
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD

Ta có:

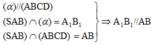
Giải bài tập Đại số 11 | Để học tốt Toán 11

⇒ A 1 B 1 là đường trung bình của tam giác SAB.

⇒ B 1 là trung điểm của SB (đpcm)

*Chứng minh tương tự ta cũng được:

• C 1 là trung điểm của SC.

• D 1 là trung điểm của SD.

b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .

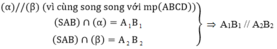
Giải bài tập Đại số 11 | Để học tốt Toán 11

⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A

⇒ B 2 là trung điểm của B 1 B

⇒ B 1 B 2 = B 2 B (đpcm)

*Chứng minh tương tự ta cũng được:

• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C

• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .

c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D

PT

Pham Trong Bach

6 tháng 12 2017

Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và (SA)=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B’ và C’. Thể tích khối chóp S.A’B’C’ bằng: A. 2 a 3 9 B. 2 a 3 27 C. a 3 9 ...

1

CM

Cao Minh Tâm

6 tháng 12 2017

PT

Pham Trong Bach

17 tháng 3 2018

Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và SA=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B' và C'. Thể tích khối chóp S.A'B'C' bằng: ...

#Toán lớp 12

1

CM

Cao Minh Tâm

17 tháng 3 2018

PT

Pham Trong Bach

1 tháng 5 2017

Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, A C = a 2 , S A ⊥ m p A B C , S A = a . Gọi G là trọng tâm tam giác SBC, mặt phẳng α đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN? ...

#Toán lớp 12

1

CM

Cao Minh Tâm

1 tháng 5 2017