Cho hình chóp S.ABCD có đáy ABCD là hình thang, A D / / B C , A D = 3 B C . M , N lần lượt là trung điểm AB; CD;G là trọng tâm. Mặt phẳng (GMN) cắt hình chóp S.ABCD theo thiết diện là
A. Hình bình hành
B. Δ G M N
C. Δ S M N
D. Ngũ giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
Ta có: MN//AD
AD\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔDSB có
O,N lần lượt là trung điểm của DB,DS
=>ON là đường trung bình của ΔDSB
=>ON//SB và \(ON=\dfrac{SB}{2}\)
Ta có: ON//SB
ON\(\subset\)(OMN)
SB không thuộc mp(OMN)
Do đó: SB//(OMN)
c: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình của ΔASC
=>OM//SC
Ta có: OM//SC
OM\(\subset\)(OMN)
SC không nằm trong mp(OMN)
Do đó: SC//(OMN)
Ta có: SB//(OMN)
SC//(OMN)
SB,SC cùng thuộc mp(SBC)
Do đó: (SBC)//(OMN)

Đáp án B
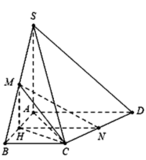
Dễ thấy ![]()
Gọi H là trung điểm của AB ![]()
Tam giác MHN vuông tại H, có 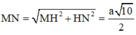
Tam giác MHC vuông tại H, có 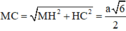
Tam giác MNC, có
c
o
s
M
N
C
^
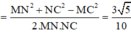
Vậy cos(MN;(SAC)) = sin M N C ^ = 1 - cos 2 M N C ^ = 55 10

Đáp án A
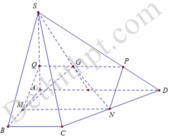
Do M N / / A D nên giao tuyến của S A D và G M N song song với AD. Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P. Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do thiết diện là hình bình hành

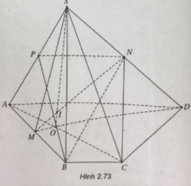
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.

a, \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\O\subset\left(SAC\right)\end{matrix}\right.\Rightarrow SO\subset\left(SAC\right)\)
\(\left\{{}\begin{matrix}S\subset\left(SBD\right)\\O\subset\left(SBD\right)\end{matrix}\right.\Rightarrow SO\subset\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Gọi \(K=AD\cap BC\)
\(\Rightarrow\left\{{}\begin{matrix}S\subset\left(SAD\right)\\K\subset\left(SAD\right)\end{matrix}\right.\Rightarrow SK\subset\left(SAD\right)\)
\(\left\{{}\begin{matrix}S\subset\left(SBC\right)\\K\subset\left(SBC\right)\end{matrix}\right.\Rightarrow SK\subset\left(SBC\right)\)
\(\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
Đáp án A
Do M N / / A D nên giao tuyến của (SAD) và (GMN) song song với AD
Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P
Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do đó thiết diện là hình bình hành