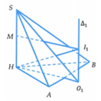
Cho hình chóp S.ABCcó mặt đáy là tam giác đều cạnh bằng 2 và hình chiếu của S lên mặt phẳng (ABC) là điểm H nằm trong tam giác ABC sao cho A H B ⏜ = 150 ° , B H C ⏜ = 120 ° , C H A ⏜ = 90 ° Biết tổng diện tích mặt cầu ngoại tiếp các hình chóp S . H A B , S . H B C , S . H C A là 124 3 π . Tính thể tích khối chóp S.ABC.
A. V S . A B C = 9 2
B. V S . A B C = 4 3
C. V S . A B C = 4 a 3
D. V S . A B C = 4

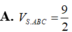
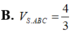

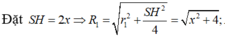
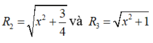

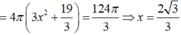


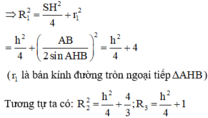

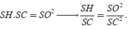
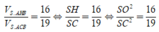
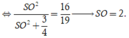
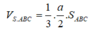
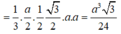
Đáp án B
Gọi r 1 , r 2 , r 3 lần lượt là bán kính đường tròn ngoại tiếp Δ H A B , Δ H B C , Δ H C A
Theo định lí Sin, ta có A B sin A H B ⏜ = 2 r 1 ⇒ r 1 = 2 2. sin 150 ° = 2 ; tương tự r 2 = 2 3 3 r 3 = 1
Gọi R 1 , R 2 , R 3 lần lượt là bán kính mặt cầu ngoại tiếp các hình chóp S . H A B , S . H B C , S . H C A
Đặt S H = 2 x ⇒ R 1 = r 1 2 + S H 2 4 = x 2 + 4 ; R 2 = x 2 + 3 4 và R 3 = x 2 + 1
Suy ra ∑ S = S 1 + S 2 + S 3 = 4 π R 1 2 + 4 π R 2 2 + 4 π R 3 2 = 4 π 3 x 2 + 19 3 = 124 π 3 ⇒ x = 2 3 3
Vậy thể tích khối chóp S.ABC là V = 1 3 . S H . S Δ A B C = 1 3 . 4 3 3 . 2 2 3 4 = 4 3
Chú ý: “Cho hình chóp S . A B C có SA vuông góc với đáy và R Δ A B C là bán kính đường tròn ngoại tiếp tam giác A B C → R = R Δ A B C 2 + S A 2 4 là bán kính mặt cầu ngoại tiếp khối chóp S.ABC”