Biết rằng đồ thị hàm số y = ( 3 a 2 - 1 ) x 3 - ( b 3 + 1 ) x 2 + 3 c 2 x + 4 d có hai điểm cực trị là (1;-7), (2:-8). Hãy xác định tổng M= a 2 + b 2 + c 2 + d 2 .
A. -18
B. 18
C. 15
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



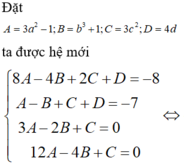
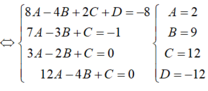
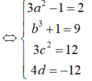


1.a
|x|+x=0
mà |x|>=0 với mọi x
=>x nhỏ hơn hoặc bằng 0
b.x+|x|=2x
=>|x|=2x-x=x
=>|x|=x
=>x>=0

các bn làm ơn giúp mk giải bài toán này ik mk đag cần nó gấp :(

Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2

Lời giải:
Vì $M\in (y=\frac{a}{x})$ nên:
$y_M=\frac{a}{x_M}\Rightarrow a=x_M.y_M=6.6=36$
Vậy hàm số có công thức $y=\frac{36}{x}(*)$
Giờ bạn thay tung độ (y) và hoành độ (x) của từng điểm vô xem có đúng với $(*)$ không thì thu được không có điểm nào thuộc ĐTHS.

a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2

a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3


Cái câu vẽ đồ thị thì bạn chỉ cần lập bảng giá trị rồi biễu diễn trên hệ trục tọa độ Oxy là được

Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.