Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe a = 2mm, khoảng cách từ hai khe đến màn ảnh D = 2m. Nguồn S phát đồng thời hai bức xạ có bước sóng λ 1 = 0 , 5 μ m và λ 2 = 0 , 4 μ m , trên đoạn MN với x M = 1 , 55 m m , x N = 9 , 5 m m . Số vân sáng của bức xạ λ 1 trùng với vân tối của bức xạ λ 2 là
A. 2
B. 4
C. 3
D. 5




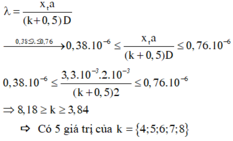
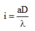
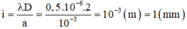
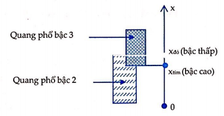
Đáp án B
Cách 1:
Dùng chức năng lập bảng của máy tính (MODE7 TABLE)
+ Tìm hàm biến này theo biến kia k2 theo biến k1 qua điều kiện trùng nhau:
Bấm = nhập giá trị của k1 theo phương trình (2)
Start? Nhập 3
End? Nhập 19
Step? Nhập 1 (vì giá trị k1, k2 nguyên)
Bấm = ta được bảng giá trị k1,k2 ta lấy các cặp giá trị nguyên.
STT
x = k 1
( f x ) = k 2
1
…
…
…
…
…
6
7
10
12
14
17
18
22