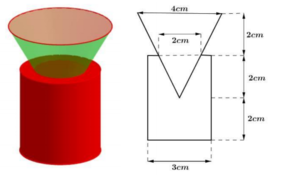
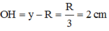Một nút chai thủy tinh là một khối tròn xoay (H), một mặt phẳng chứa trục của (H) cắt (H) theo một thiết cho trong hình vẽ dưới. Tính thể tích của (H) (đơn vị: c m 3 )?
A. V H = 41 3 π
B. V H = 13 π
C. V H = 23 π
D. V H = 17 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
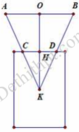
Xét mặt cắt và đặt tên các điểm như hình vẽ
Thể tích khối trụ là V 1 = π r 1 2 h t = π 1 , 5 2 .4 = 9 π
Ta có: C D A B = H K O K ⇒ O K = 4 ⇒ H K = 2
Thể tích khối nón cụt là V n = π O A 2 O K 3 − π C H 2 H K 3 = 14 π 3
Thể tích của H là: V t + V n = 41 π 3

Chọn B.
Phương pháp:
Thiết diện qua trục của hình trụ có bán kính đáy R và chiều cao h là hình chữ nhật có kích thước 2R × h. Thể tích khối trụ bán kính đáy R và chiều cao h là V = πR 2 h .
Cách giải:
Một mặt phẳng qua trục cắt khối trụ theo thiết diện là một hình chữ nhật có diện tích bằng 16a2
⇒ 2 R . 2 R = 16 a 2 ⇔ R 2 = 4 a 2 ⇔ R = 2 a ⇒ h = 2 R = 4 a
Thể tích của khối trụ đã cho: V = πR 2 h = π . ( 2 a ) 2 . 4 a = 16 πa 3 .

Đáp án A
Thể tích vật thể tạo thành khi quay phần hình phẳng giới hạn bởi hai đồ thị hàm số y = f (x) ; y = g (x) và
hai đường thẳng x = a; x = b quanh trục Ox là V = π ∫ a b f 2 x - g 2 x d x
Cách giải:
Ta có :
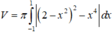
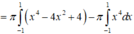

Đáp án A
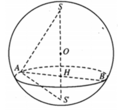
Kí hiệu bán kính đáy của hình nón là x, chiều cao hình nón là y (trong đó 0<x≤2R; 0<y≤R). Gọi SS’là đường kính của mặt cầu ngoại tiếp hình nón thì ta có:
![]() (hệ thức lượng trong tam giác vuông)
(hệ thức lượng trong tam giác vuông)
Gọi V1 là thể tích khối nón: 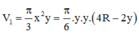
Mặt khác 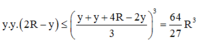
Do đó 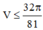 dấu bằng xảy ra
dấu bằng xảy ra ![]()
Khi đó