Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị của hàm số cắt Ox tại điểm (2;0) như hình vẽ. Hàm số đồng biến trên khoảng nào sau đây?
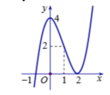
A. (-1;+ ∞ )
B. (- ∞ ;0)
C. (-2;0)
D. (- ∞ ;-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Tập xác định của hàm số y=f(x) là D=R Từ đồ thị đã cho ta có: f ' ' x = 0 ⇔ x = - 1 x = 2 .
Bảng biến thiên.
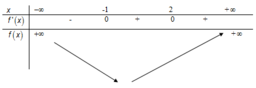
Dựa vào bảng biến thiên của hàm số y=f(x) ta nhận thấy hàm số y=f(x) đồng biến trên khoảng
-
1
;
+
∞
.

Ta có: f' (x - 2) = f' (x).(x-2)' = f'(x)
Do đó; đồ thị hàm số y= f’ (x) có hình dạng tương tự như trên.
Đồ thị hàm số y= f( x-2) có 3 điểm cực trị khi và chỉ khi đồ thị hàm số y= f( x) cũng có 3 điểm cực trị.
Chọn D.

Đáp án D
Phương pháp : Nhận xét : f’(x – 2) = f’(x)
Cách giải : Ta có : f’(x – 2) = (x – 2)’. f’(x) = f’(x) → Đồ thị hàm số y = f’(x) có hình dạng tương tự như trên.
Đồ thị hàm số y = f(x – 2)có 3 điểm cực trị => Đồ thị hàm số y = f(x) cũng có 3 điểm cực trị
Chọn A.
Tập xác định của hàm số y = f(x) là D = ℝ . Từ đồ thị đã cho ta có: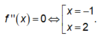
Bảng biến thiên
Dựa vào bảng biến thiên của hàm số ta nhận thấy hàm số y = f(x) đồng biến trên khoảng (-1;+ ∞ )