Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có
A
B
=
4
c
m
. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với
A
B
C
. Lấy M thuộc SC sao cho
C
M
=
2
M
S
. Khoảng cách giữa hai đường AC và BM là A.
4
21
7
c
m
B.
8
13
c
m
C.
9
21
7
c
m
D....
Đọc tiếp
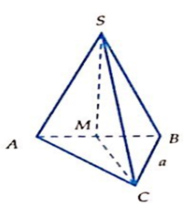
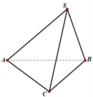
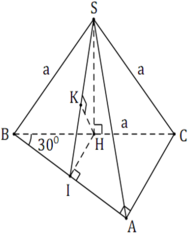
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có A B = 4 c m . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với A B C . Lấy M thuộc SC sao cho C M = 2 M S . Khoảng cách giữa hai đường AC và BM là
A. 4 21 7 c m
B. 8 13 c m
C. 9 21 7 c m
D. 2 10 3 c m
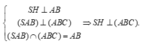
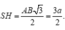
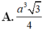
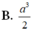
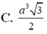
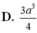
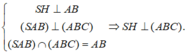
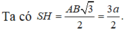
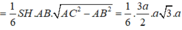
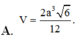
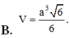
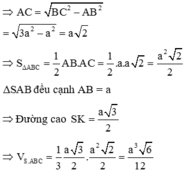
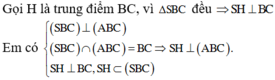
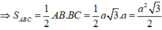
Chọn A.
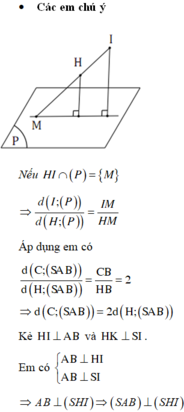
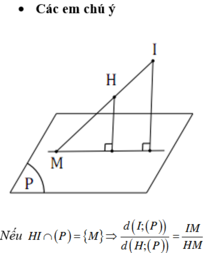
Phương pháp : Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này tới mặt phẳng chứa đường thẳng kia và song song với đường thẳng này.
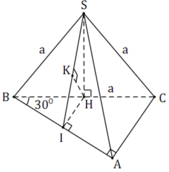
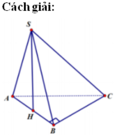
Cách giải : Qua M dựng đường thẳng song song với AC cắt SA tại E.
Gọi H là trung điểm AB.
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy nên S H ⊥ A B C