Giá trị của m để đồ thị hàm y = x 4 + 2 m x 2 - 1 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 4 2 là:
A. m = 2
B. m = ± 2
C. m = - 2
D. m = - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án D.
Có y ' = 4 x 3 − 4 m x ; y ' = 0 ⇔ x = 0 x = m x = − m
(xét trong trường hợp nó có 3 cực trị thì m>0)
Khi đó 3 điểm cực trị là;
A 0 ; 2 ; B m ; 2 − m 2 ; C − m ; 2 − m 2 .
A,B,C lập thành một tam giác có diện tích bằng 1 nếu
S A B C = 1 ⇔ 1 2 A H . B C = 1 ⇔ 1 2 2 m − m 2 = 1 ⇔ m = 1.

Đáp án A

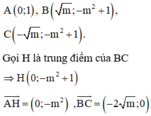
Tam giác ABC cân tại A, do đó diện tích tam giác ABC là
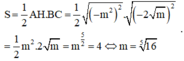

\(y'=4x^3-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=m\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A; B; C với \(\left\{{}\begin{matrix}A\left(0;m^4+2m\right)\\B\left(\sqrt{m};2m\right)\\C\left(-\sqrt{m};2m\right)\end{matrix}\right.\)
Tam giác ABC luôn cân tại A, gọi H là trung điểm BC \(\Rightarrow H\left(0;2m\right)\)
\(AH=\left|y_A-y_H\right|=m^4\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{m}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.m^4.2\sqrt{m}=4\)
\(\Leftrightarrow m^9=16\Rightarrow m=\sqrt[3]{2}\)