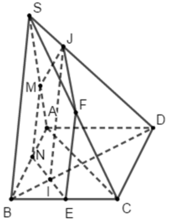
Cho hình chóp S.ABCD có AC và BD cắt nhau tại E; AB và CD cắt nhau tại F. Gọi M, N lần lượt là các điểm trên các đoạn thẳng SA,SB sao cho đường thẳng MN cắt đường thẳng SF, AB tại hai điểm khác nhau. Tìm giao tuyến của mặt phẳng (EMN ) với các mặt của hình chóp đã cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Lời giải:
$\widehat{BAD}=60^0\Rightarrow \widehat{BAO}=30^0$
$\frac{BO}{AB}=\sin \widehat{BAO}=\sin 30^0=\frac{1}{2}$
$\Rightarrow BO=\frac{AB}{2}=\frac{a}{2}$
$BD=2BO=a$
$\frac{AO}{AB}=\cos \widehat{BAO}=\cos 30^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AO=\frac{\sqrt{3}a}{2}$
$\Rightarrow AC=\sqrt{3}a$
$S_{ABCD}=\frac{BD.AC}{2}=\frac{\sqrt{3}a^2}{2}$
$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3a}{4}.\frac{\sqrt{3}a^2}{2}=\frac{\sqrt{3}a^3}{8}$
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Tham khảo hình vẽ:
a) • Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {IC{\rm{D}}} \right)\\M \in SA \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow M \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\C \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\end{array}\)
\( \Rightarrow M,I,C\) thẳng hàng.
Do đó \(M\) là giao điểm của \(IC\) và \(SA\).
• Ta có:
\(\begin{array}{l}\left. \begin{array}{l}N \in \left( {IC{\rm{D}}} \right)\\N \in SB \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow N \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\D \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
\( \Rightarrow N,I,D\) thẳng hàng.
Do đó \(N\) là giao điểm của \(I{\rm{D}}\) và \(SB\).
• Ta có:
\(\begin{array}{l}AB = \left( {SAB} \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {IC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {SAB} \right) \cap \left( {IC{\rm{D}}} \right)\\AB\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(AB\parallel C{\rm{D}}\parallel MN\).
Áp dụng định lí Medelaus cho tam giác \(SOA\) với cát tuyến \(CIM\), ta có:
\(\frac{{SM}}{{MA}}.\frac{{AC}}{{OC}}.\frac{{OI}}{{SI}} = 1 \Leftrightarrow \frac{{SM}}{{MA}}.2.1 = 1 \Leftrightarrow \frac{{SM}}{{MA}} = \frac{1}{2}\)
Xét tam giác \(SAB\) có \(MN\parallel AB\). Theo định lí Thales ta có:
\(\frac{{MN}}{{AB}} = \frac{{SM}}{{MA}} = \frac{1}{2} \Leftrightarrow MN = \frac{1}{2}AB = \frac{a}{2}\)
b) Ta có:
\(\begin{array}{l}BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\SK = \left( {SAD} \right) \cap \left( {SBC} \right)\\AD\parallel BC\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(SK\parallel BC\parallel A{\rm{D}}\).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
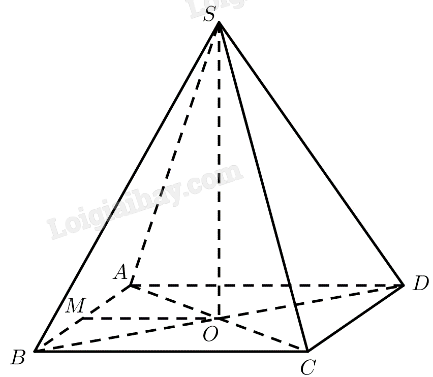
a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)
\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)
b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)
\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)
Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)
\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)
\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)
\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
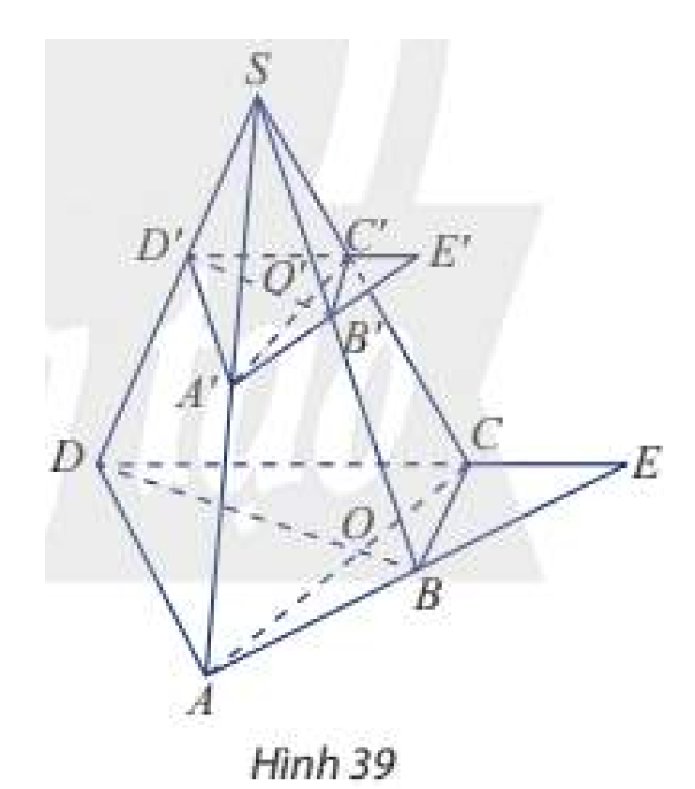
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}O' \in A'C' \subset \left( {SAC} \right)\\O' \in B'D' \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O' \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Do đó, \(S,O,O'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Vậy \(S,O',O\) thẳng hàng.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\\left. \begin{array}{l}E' \in A'B' \subset \left( {SAB} \right)\\E' \in C'D' \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E' \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\)
Do đó, \(S,E,E'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\).
Vậy \(S,E,E'\) thẳng hàng.
CM
14 tháng 9 2017
Đáp án D
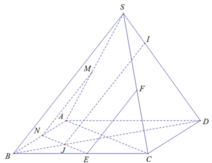
Gọi M là điểm bất kì trên cạnh SA
Trong (SAB), kẻ Mx // SB, Mx cắt AB tại N
Trong (ABCD), kẻ Ny // AC, Ny cắt BC tại E
Ny cắt BD tại J
Trong (SBC), kẻ Ez // SB, Ez cắt SC tại F
Trong (SBD), kẻ Jt // SB, Jt cắt SD tại I
⇒ IJ // (SAB)