Cho hàm số y= f(x) liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình vẽ.
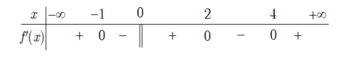
Hàm số y= f(x) có bao nhiêu điểm cực trị?
A. 4.
B. 1.
C. 2.
D. 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Dựa vào bảng xét dấu ta thấy hàm số đổi dấu qua các điểm x = − 1 , x = 0 , x = 2 , x = 4 nên hàm số có 4 điểm cực trị.

Nhận thấy y' đổi dấu khi qua x = -3 và x = 2 nên hàm số có 2 điểm cực trị. ( x = 1 không phải là điểm cực trị vì y' không đổi dấu khi qua x = 1). Chọn C.

Chọn A.
Phương pháp:
Điểm x = x0 là điểm cực trị của hàm số khi qua điểm đó f'(x) đổi dấu.
Cách giải :
Dựa vào BXD ta thấy hàm số có 4 điểm cực trị x = -1; x = 0; x = 2; x = 4.
Chú ý: Nhiều học sinh cho rằng x = 0 không phải là điểm cực trị do y' (0) ≠ 0. Lưu ý điều kiện f'(x0) = 0
chỉ là điều kiện cần để x = x0 là điểm cực trị của hàm số.

Dựa vào bảng biến thiên ta thấy rằng f’(-2)=f’(1)=f’(3)=0.
f’(x)đổi dấu khi qua hai điểm x=-2; x=3 và f’(x) không đổi dấu khi qua điểm x=1 nên hàm số y=f(x) có hai diểm cực trị.
Đáp án A

Vì hàm số xác định trên cả R và y' đổi dấu khi đi qua các điểm -2;-1;1;2 do đó hàm số có 4 điểm cực trị.
Chọn đáp án B.

Đáp án D
Dựa vào bảng xét dấu f ' (x) ta có: hàm số f(x) liên tục trên ℝ có 4 điểm x o mà tại đó f ' (x) đổi dấu khi x qua điểm x o . Vậy hàm số đã cho có 4 điểm cực trị
Đáp án là A
Hàm số có 4 điểm cực trị