Sau một tháng thi công thì công trình xây dựng Nhà học thể dục của trường THPT Toàn Thắng đã thực hiện được một khối lượng công việc. Nếu vẫn tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công trình và kịp đưa vào sử dụng, công ty xây dựng quyết định từ tháng thứ hai, mỗi tháng tăng 4% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công?
A. 19
B.18
C. 17
D. 20

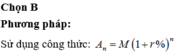
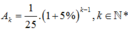

Chọn B