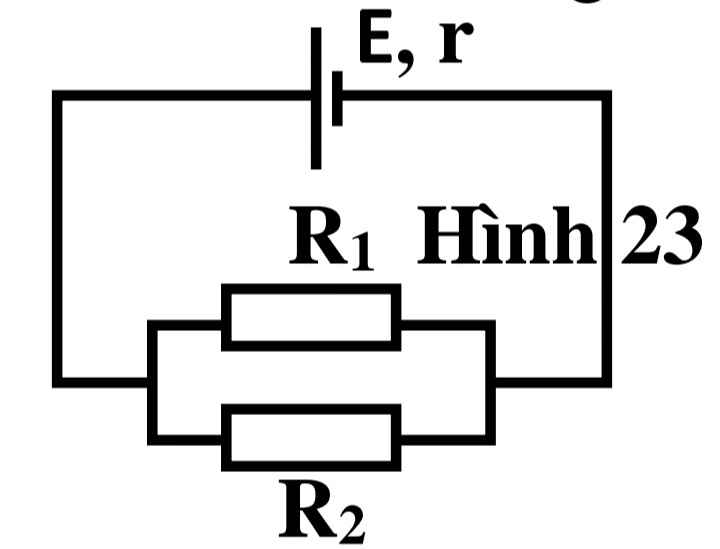
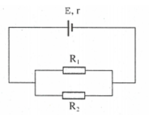
Nguồn điện có suất điện động E = 24V, điện trở trong r = 4. Điện trở R1 = 6. Tính R2 để:
a. Công suất mạch ngoài lớn nhất. Tính công suất của nguồn khi đó.
b. Công suất trên R2 lớn nhất. Tính công suất này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Công suất mạch ngoài: \(P=I^2(R_1+R_2)\), mà \(I=\dfrac{E}{R_1+R_2+r}\)
\(\Rightarrow P= (\dfrac{E}{R_1+R_2+r})^2.(R_1+R_2)\), Đặt \(x=R_1+R_2\)
\(\Rightarrow P= (\dfrac{E}{x+r})^2.x=\dfrac{E^2x}{x^2+2xr+r^2}=\dfrac{E^2}{x+\dfrac{r^2}{x}+2r}\)
Pmax khi mẫu số min, mà \(x+\dfrac{r^2}{x}\ge 2\sqrt{x.\dfrac{r^2}{x}}=2r\)(dẫu '=' xảy ra khi \(x=r\))
Vậy \(P_{max}=\dfrac{E^2}{4r}=18W\), khi \(R_1+R_2=R \) \(\Rightarrow R_2=1,5\Omega\)
b. Làm tương tự
Công suất trên R2: \(P_2=I^2.R_2=(\dfrac{E}{R_1+r+R_2})^2.R_2\)
\(\Rightarrow P_2=\dfrac{E^2.R_2}{(R_1+r)^2+2.(R_1+r)R_2+R_2^2}\)
\(\Rightarrow P_2=\dfrac{E^2}{\dfrac{(R_1+r)^2}{R_2}+R_2+2.(R_1+r)}\)
P2 max khi mẫu số min, mà theo BĐT cô si ta có: \(\dfrac{(R_1+r)^2}{R_2}+R_2 \ge 2(R_1+r)\), dấu '=' xảy ra khi: \(\dfrac{(R_1+r)^2}{R_2}=R_2\)\(\Rightarrow R_2=R_1+r=2,5\Omega\)
\(P_{2max}=\dfrac{E^2}{4(R_1+r)}=14,4W\)
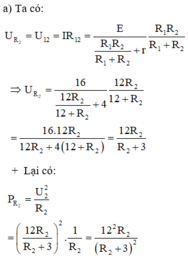
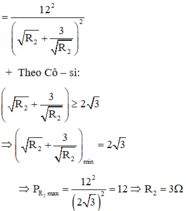
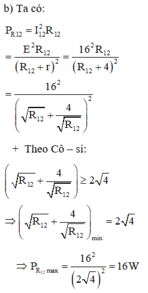



b)Công suất tiêu thụ trên mạch 2:
\(P_2=\left(\dfrac{\xi}{r+R_1+R_2}\right)^2\cdot R_2=\left(\dfrac{24}{4+6+R_2}\right)^2\cdot R_2=\left(\dfrac{24}{10+R_2}\right)^2\cdot R_2\) Áp dụng bđt Cô-sy:
\(P_2=\dfrac{24^2}{(\dfrac{10}{\sqrt{R_2}}+\sqrt{R_2})^2}\le\dfrac{24^2}{10\cdot4}=14,4W\)
Dấu "=" xảy ra\(\Leftrightarrow10=R_2\)
a)Công suất tiêu thụ mạch ngoài:
\(P_N=\left(\dfrac{\xi}{r+R_N}\right)^2\cdot R_N=\dfrac{\xi^2}{\left(\dfrac{r}{\sqrt{R_N}}+\sqrt{R_N}\right)^2}\le\dfrac{\xi^2}{4r}=\dfrac{24^2}{4\cdot4}=36\)
(Bất đẳng thức Cô-sy)
Dấu "=" xảy ra\(\Leftrightarrow r=R_N=4\Omega\)
\(\Rightarrow\dfrac{1}{4}=\dfrac{1}{6}+\dfrac{1}{R_2}\Rightarrow R_2=12\Omega\)