Tìm tất cả các giá trị của tham số m để hàm số f x = 4 sin x + 6 m + sin x 9 sin x + 4 1 + sin x có giá trị lớn nhất không nhỏ hơn 1 3
A. m ≥ log 6 2 3
B. m ≥ log 6 13 18
C. m ≤ log 6 3
D. m ≤ log 6 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Ta có y ' = cos x − m .
Hàm số nghịch biến trên R
⇔ y ' ≤ 0 , ∀ x ∈ ℝ ⇒ cos x − m ≤ 0 ∀ x ∈ ℝ ⇔ cos x ≤ m ∀ x ∈ ℝ ⇒ m ≥ M a x ℝ cos x = 1.
1.
ĐKXĐ: \(1-x^2>0\Leftrightarrow0< x< 1\)
Pt tương đương:
\(x=5-2m\)
Pt có nghiệm khi và chỉ khi:
\(0< 5-2m< 1\) \(\Leftrightarrow2< m< \dfrac{5}{2}\)
2.
\(M=\dfrac{\dfrac{sina.cosa}{cos^2a}}{\dfrac{sin^2a}{cos^2a}-\dfrac{cos^2a}{cos^2a}}=\dfrac{tana}{tan^2a-1}=\dfrac{\left(-\dfrac{2}{3}\right)}{\left(-\dfrac{2}{3}\right)^2-1}=-\dfrac{6}{5}\)
Chọn A
Đặt 
ta có: 
Ta có 
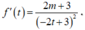
Do m ∈ Z nên ta xét hai trường hợp sau
+TH1: 
thì hàm số đồng biến trên [-1;1].
Xét 
+TH2: 
thì hàm số nghịch biến trên [-1;1]
Xét 
Vậy 
Vậy tập S có 4 phần tử.
Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số:
Để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]
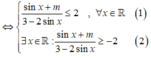
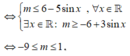
Đáp án A
f x = 4 sin x + 6 m + sin x 9 sin x + 4 1 + sin x = 2 3 2 sin x + 6 m . 2 3 sin x 1 + 4. 2 3 2 sin x ,
đặt t = 2 3 sin x
⇒ f t = t 2 + n t 1 + 4 t 2 với 2 3 ≤ t ≤ 3 2 n = 6 m > 0
Bài toán trở thành tìm n >0 để f t ≥ 1 3 với t ∈ 2 3 ; 3 2
⇒ f t ≥ 1 3 ⇔ t 2 + n t 1 + 4 t 2 ≥ 1 3 ⇔ n ≥ t 3 + 1 3 t
Xét g t = t 3 + 1 3 t trên đoạn 2 3 ; 3 2 có min 2 3 ; 3 2 t = g 1 = 2 3
Theo bài ra ⇒ g t ≤ n phải có nghiệm trên 2 3 ; 3 2
⇔ n ≥ min 2 3 ; 3 2 g t ⇔ n ≥ 2 3 ⇔ m ≥ log 6 2 3