Cho hình bs 12
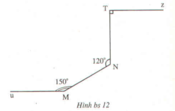
Chứng minh rằng đường thẳng Mu song song với đường thẳng Tz
Mỗi bài từ số I.4 đến số I.10 sau đây đều có bốn lựa chọn là (A), (B), (C) và (D) nhưng chỉ có một trong số đó là đúng. Hãy chọn phương án đúng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

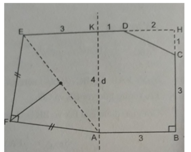
Gọi H là giao điểm của hai đường thẳng ED và BC. Khi đó, ABHE là hình thang và tính được diện tích của nó là
S 1 = 1/2 (AB + EH).BH = 1/2 (3 + 6).4 = 18( c m 2 ).
Diện tích của tam giác vuông DHC là
S 2 = 1/2 DH.CH = 1/2.2.1 = 1( c m 2 ).
Trong tam giác vuông AKE tính được EA = 5 (cm).
Trong tam giác vuông FEA có FE = FA suy ra E F 2 = 25/2.
Từ đó diện tích của tam giác FAE là S 3 = 25/4 c m 2
Vậy diện tích của lục giác đã cho là
S = S 3 + S 1 - S 2 = 25/4 + 18 – 1 = 93/4( c m 2 ).

1)hãy đặt các dấu ngoặc vào vế trái để đẳng thức sau trở nên đúng
1:2:3:4:5:6:7:8:9:10=7
Đáp án:
Xét vế trái của đẳng thức sau: 1 : 2 : 3 : 4 : 5 : 6 : 7 : 8 : 9 : 10 = 7.
Do 7 là số nguyên tố lớn nhất trong các số xuất hiện nên để có đẳng thức đúng thì 7 phải nằm ở tử số. Trong mọi trường hợp đặt ngoặc đơn, ta có 1 luôn nằm ở tử số và 2 luôn nằm ở mẫu số.
Để ý rằng 2 x 5 = 10; 3 x 8 = 4 x 6 = 24; 9 = 3 x 3;
và 720 = 10 x 9 x 8 = 10 x 9 x 2 x 4 = 10 x 6 x 4 x 3.
Từ đó suy ra có 3 cách thêm dấu ngoặc đơn như sau:
Cách 1: Có 7, 8, 9, 10 nằm ở tử số: 1 : 2 : 3 : 4 : 5 : (6 : 7 : 8 : 9 : 10) = 7.
Cách 2: Có 3, 5, 6, 7, 8 nằm ở tử số: 1 : (2 : 3) : (4 : 5 : 6 : 7 : 8) : 9 : 10 = 7.
Cách 3: Có 3, 4, 6, 7, 10 nằm ở tử số: 1 : (2 : 3 : 4) : (5 : 6 : 7) : 8 : (9 : 10) = 7.
mình mới cop

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Trong trường hợp hình d) thì a và b không song song với nhau vì tổng hai góc trong cùng phía không bằng 180°

Ta biết rằng có duy nhất một đường thẳng đi qua một điểm cho trước, vuông góc với một đường thẳng cho trước và có vô số đường thẳng đi qua một điểm cho trước cắt một đường cho trước. Bởi vì, có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d và có vô số đường xiên kẻ từ điểm A đến đường thẳng d.
(A) Đúng
(B) Sai
(C) Sai
(D) Đúng
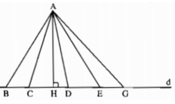
Trong hình AH là đường vuông góc duy nhất và AB, AC, AD, AE, AG là những đường xiên kẻ từ A đến d (có thể kẻ được vô số đường xiên như thế)

a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp
Bài này có nhiều cách giải, ta có thể làm theo cách sau đây.
Từ điểm M vẽ đường thẳng Mn song song với đường thẳng TN.
+) Khi đó, vì ∠TNM + ∠NMn = 180° (hai góc trong cùng phía)
Mà ∠TNM = 120° nên ∠NMn = 60°.
+) Vẽ Mu’ là tia đối của Mu, biết ∠uMN = 150° nên tính được ∠NMu' = 30°.
Vì ∠uMN + ∠NMu’ = 180° (hai góc kề bù) biết ∠uMN = 150° nên tính được ∠NMu' = 30°.
Từ đó ∠nMu' = ∠NMn + ∠NMu' = 60° + 30° = 90°, tức là đường thẳng Mn vuông góc với đường thẳng Mu.
Do đường thẳng Mn song song với đường thẳng TN nên suy ra đường thẳng TN cũng vuông góc với đường thẳng Mu.
Từ đó Tz song song với Mu vì cùng vuông góc với TN.