Trong không gian Oxyz , tìm tất cả các giá trị của tham số m để phương trình x 2 + y 2 + z 2 + 2 x - 4 y + 4 z + m = 0 là phương trình của một mặt cầu.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8

Đáp án C
Mặt cầu (S) tâm I(2;-1;-2) và bán kính R =2. Để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung thì

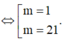

Đáp án C
Mặt cầu (S)tâm I 2 ; − 1 ; − 2 và bán kính R = 2. . Để mặt phẳng (P)và mặt cầu (S)có đúng 1 điểm chung thì d I ; P = R ⇔ 4.2 − 3 − 1 − m 4 2 + 3 2 = 2 ⇔ m = 1 m = 21 .

Đáp án A
Ta có:
![]()
Mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R) khi và chỉ khi
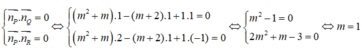

Đáp án là C.
Để phương trình đã cho là phương trình mặt cầu thì
![]()
![]()

Chọn đáp án B

MEMORIZE |
Vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. |

Chọn C.