Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 2 = y + 1 2 = z 3 ; ∆ 2 : x - 3 - 1 = y - 3 - 2 = z + 2 1
A. ∆ 1 song song với ∆ 2 .
B. ∆ 1 chéo với ∆ 2 .
C. ∆ 1 cắt ∆ 2 .
D. ∆ 1 trùng với ∆ 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
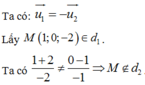
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C

Đáp án B
Ta có
u 1 → = 2 ; 3 ; 2 , u 2 → − 2 ; 2 ; − 3 , M 1 1 ; − 2 ; 2 , M 2 − 2 ; 2 ; 3 .
u 1 → , u 2 → . M 1 M 2 → = 57 ≠ 0.
Vậy d 1 và d 2 chéo nhau.

Đáp án B
Đường thẳng d 1 đi qua điểm M 1 (2; 0; -1) và có vectơ chỉ phương là u 1 → = (4; -6; -8);
đường thẳng d 2 đi qua điểm M 2 (7; 2; 0) và có vectơ chỉ phương là u 2 → = (-6; 9; 12).
Do hai vectơ u 1 → và u 2 → cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M 1 vào d 2 , ta thấy:
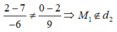
Do đó hai đường thẳng d 1 và d 2 song song.
Vậy đáp án B là đúng.

Đáp án A
Đường thẳng d có véc-tơ chỉ phương ![]() = (3;-1;-2) và đi qua điểm M(-1;0;1).
= (3;-1;-2) và đi qua điểm M(-1;0;1).
Đường thẳng d' có véc-tơ chỉ phương ![]() =(-3;1;2).
=(-3;1;2).
Hai véc-tơ ![]() và
và ![]() cùng phương và điểm M không thuộc đường thẳng d'.
cùng phương và điểm M không thuộc đường thẳng d'.
Do đó hai đường thẳng d và d' song song với nhau.

Đường thẳng d qua M ( 2;-4;1 ) và có vectơ chỉ phương là u → 2 ; 3 ; 2
Đường thẳng d’ qua M' ( 0;1;-1 ) và có vectơ chỉ phương là u ' → = 4 ; 6 ; 4
Do u → và u ' → cùng phương đồng thời M ∉ d ' nên hai đường thẳng đó song song nhau.
Đáp án A
Chọn C