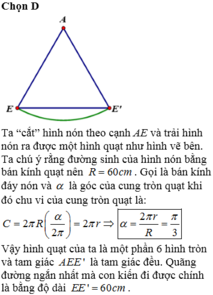
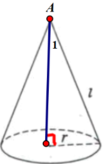
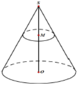
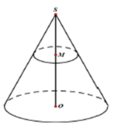
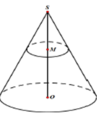
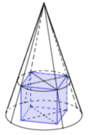
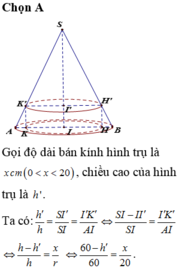
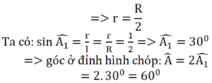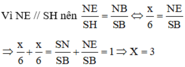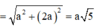Một cây thông Noel có dạnh hình nón với chiều dài đường sinh bằng 60cm và bán kính đáy r=10cm. Một chú kiến bắt đầu xuất phát từ một đỉnh nằm trên mặt đáy hình nón và có dự định bò một vòng quanh cây thông sau đó quay trở lại vị trí xuất phát ban đầu. Tính quãng đường ngắn nhất mà chú kiến có thể đi được là bao nhiêu?
![]()
![]()
![]()
![]()