2x3 + 6x2 = x2 +3x
Giari chi tiết giùm nhé :*
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(-\left(-3x^2\right)^3+4x-9-27x^6\)
\(=27x^6-27x^6+4x-9\)
=4x-9
=-1

Câu 6:Thực hiện phép nhân -2x(x2 + 3x - 4) ta được:
A.-2x3 - 6x2 – 8x B. 2x3 -6x2 – 8x C. -2x3 - 6x2 + 8x D. -2x3 + 3x2 -4
Câu 7 : Phân tích đa thức x2 + 2xy + y2 – 9z2 thành nhân tử ta được:
A. (x+y+3z)(x+y–3z)
B. (x-y+3z)(x+y–3z)
C.(x - y +3z)(x - y – 3z)
D. (x + y +3z)(x -y – 3z)
Câu 9: Phân tích đa thức x2 + 7x + 12 thành nhân tử ta được:
A. (x - 3)( x + 4 ) B. (x + 3)( x + 4 ) C.(x + 5)( x + 2 ) D. (x -5)( x + 2 )
Câu 10: Giá trị của biểu thức (x2 + 4x + 4) tại x = - 2 là:
A. 4 B. -2 C. 0 D. -8
Mấy câu còn lại bị lỗi r nhé

2x3 + 6x2 = x2 + 3x
⇔ (2x3 + 6x2) – (x2 + 3x) = 0
⇔ 2x2(x + 3) – x(x + 3) = 0
⇔ x(x + 3)(2x – 1) = 0
(Nhân tử chung là x(x + 3))
⇔ x = 0 hoặc x + 3 = 0 hoặc 2x – 1 = 0
+ x + 3 = 0 ⇔ x = -3.
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
Vậy tập nghiệm của phương trình là 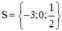

a) 6x2 . (2x3 – 3x2 + 5x – 4)
= 6x2 . 2x3 +6x2 . (-3x2) + 6x2 . 5x + 6x2 .(-4)
= 12x5 – 18x4 + 30x3 – 24x2
b) (-1,2x2) . (2,5x4 – 2x3 + x2 – 1,5)
= (-1,2x2) . 2,5x4 + (-1,2x2) . (-2x3) + (-1,2x2) . x2 + (-1,2x2) . (-1,5)
= -3x6 + 2,4x5 – 1,2x4 + 1,8x2

a, \(x^4-x^2-2=0\Leftrightarrow x^4-2x^2+x^2-2=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(x^2-2\right)=0\Leftrightarrow\left(x^2+1>0\right)\left(x^2-2\right)=0\Leftrightarrow x=\pm\sqrt{2}\)
b, \(\Leftrightarrow x^2\left(x^2+2x+1\right)=0\Leftrightarrow x^2\left(x+1\right)^2=0\Leftrightarrow x=0;x=-1\)
c, \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1>0\right)=0\Leftrightarrow x=1\)
d, \(\Leftrightarrow6x^2-3x-4x+2=0\Leftrightarrow\left(3x-2\right)\left(2x-1\right)=0\Leftrightarrow x=\dfrac{2}{3};x=\dfrac{1}{2}\)
a)
/ \(x^4+x^2-2=0\)
\(\Leftrightarrow\left(x^2\right)^2-x^2+2x^2-2=0\\ \Leftrightarrow x^2\left(x^2-1\right)+2\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2=0\\x+1=0\\x-1-0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

a: \(\left(3x-2\right)\left(2x-1\right)-\left(6x^2-3x\right)=0\)
\(\Leftrightarrow6x^2-3x-4x+2-6x^2+3x=0\)
\(\Leftrightarrow-4x=-2\)
hay \(x=\dfrac{1}{2}\)
b: \(x^3-\left(x+1\right)\left(x^2-x+1\right)=x\)
\(\Leftrightarrow x=x^3-x^3-1\)
hay x=-1

a) Ta có: \(x^3+x^2+x+1=0\)
\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
mà \(x^2+1>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
b) Ta có: \(x^3-6x^2+11x-6=0\)
\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6=0\)
\(\Leftrightarrow x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)
Vậy: S={1;2;3}
c) Ta có: \(x^3-x^2-21x+45=0\)
\(\Leftrightarrow x^3-3x^2+2x^2-6x-15x+45=0\)
\(\Leftrightarrow x^2\left(x-3\right)+2x\left(x-3\right)-15\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+2x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+5x-3x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
Vậy: S={3;-5}
d) Ta có: \(x^4+2x^3-4x^2-5x-6=0\)
\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+4x^2-8x+3x-6=0\)
\(\Leftrightarrow x^3\left(x-2\right)+4x^2\cdot\left(x-2\right)+4x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+3x^2+x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+3\right)+\left(x+1\right)\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)\left(x^2+x+1\right)=0\)
mà \(x^2+x+1>0\forall x\)
nên (x-2)(x+3)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy: S={2;-3}

`2x^3 +6x^2 =x^2 +3x`
`<=> 2x^3 +6x^2 -x^2 -3x=0`
`<=> 2x^3 +5x^2 -3x=0`
`<=> x(2x^2 +5x-3)=0`
`<=> x(2x^2 +6x-x-3)=0`
`<=> x[2x(x+3)-(x+3)]=0`
`<=> x(2x-1)(x+3)=0`
\(< =>\left[{}\begin{matrix}x=0\\2x-1=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
b)
`(2+x)^2 -(2x-5)^2=0`
`<=> (2+x-2x+5)(2+x+2x-5)=0`
`<=> (-x+7)(3x-3)=0`
\(< =>\left[{}\begin{matrix}-x+7=0\\3x-3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
`a) 2x^3 + 6x^2 = x^2 + 3x`
`=> 2x^3 + 6x^2 - x^2 - 3x = 0`
`=> 2x^3 + 5x^2 - 3x = 0`
`=> x(2x^2 + 5x - 3) = 0`
`=> x (2x^2 + 6x - x - 3) = 0`
`=> x [(2x^2 + 6x) - (x+3)] = 0`
`=> x [2x(x+3) - (x+3)] = 0`
`=> x (2x - 1)(x+3) = 0`
`=> x = 0` hoặc `2x - 1 = 0` hoặc `x + 3 = 0`
`=> x = 0` hoặc `x = 1/2` hoặc `x = -3`
`b) (2+x)^2 - (2x-5)^2 = 0`
`=> (2+x+2x-5)(2+x-2x+5) = 0`
`=> (3x - 3)(7-x) = 0`
`=> 3x - 3 = 0` hoặc `7 - x = 0`
`=> x = 1` hoặc `x = 7`

2)
a)
chiều dài ADN: L=N/2*3.4=5100A
chu kì vòng xoắn: c=N/20=150
b)
Nu loại A chiếm 20%=> A=T=3000.20%=600
từ Nu loại A = 20%=> Nu loại G= 30%=> G=X=900
số lk H= 2A+3G= 2*600+3*900=3900
2x^3+6x^2=x^2+3x
=>2x^3+6x^2-x^2-3x=0
=>2x^3+5x^2-3x=0
=>x(2x^2+5x-3)=0
=>x=0 hoặc 2x^2+5x-3=0
=>x=0 , 2x^2-x+6x-3=0
=>x=0 , x(2x-1)+3(2x-1)=0
=>x=0 , (2x-1)(x+3)=0
=>x=0 , 2x-1=0 hoac x+3=0
=> x=0 , x=1/2 ,x=-3
giải ra giùm cái đy chi tiết vô