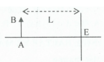
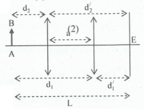
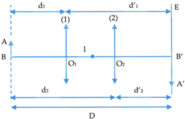
Một vật sáng AB hình mũi tên đặt song song với một màn E như hình bên. Khoảng cách giữa AB và E là L = 90 cm. Giữa AB và E có một thấu kính hội tụ tiêu cự f. Tịnh tiến thấu kính dọc theo trục chính AE người ta thấy có hai vị trí của thấu kính đều cho ảnh rõ nét của AB trên màn. Biết khoảng cách giữa hai vị trí của thấu kính là a = 30 cm. Tìm tiêu cự f của thấu kính.
A. 45 cm
B. 40 cm
C. 30 cm
D. 20 cm

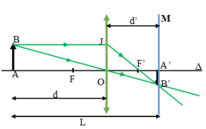

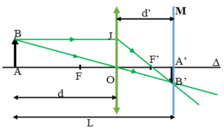





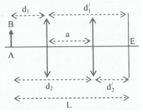


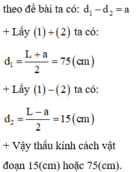




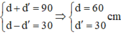
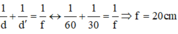
+ Theo tính thuận nghịch của chiều truyền ánh sáng ta có: