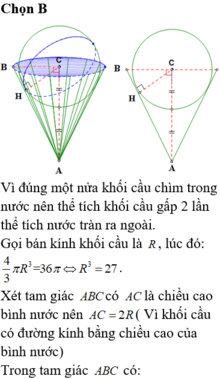
Một vật thể đựng đầy nước hình lập phương không có nắp. Khi thả một khối cầu kim loại đặc vào trong hình lập phương thì thấy khối cầu tiếp xúc với tất cả các mặt của hình lập phương đó. Tính bán kính của khối cầu, biết thể tích nước còn lại trong hình lập phương là 10. Giả sử các mặt của hình lập phương có độ dày không đáng kể.
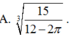
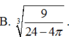
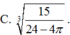
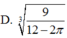

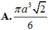







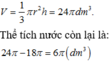
Đáp án đúng : A