Cho hình chóp đều S.ABCD có AC = 2a, góc giữa mặt phẳng (SBC) và mặt đáy bằng 45 ° . Thể tích của khối chóp S.ABCD bằng:
A. a 3 2 .
B. 2 3 a 3 3 .
C. a 3 2 3 .
D. a 3 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
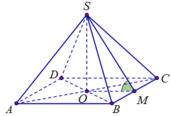
Gọi M là trung điểm của BC, suy ra O M ⊥ B C .
Ta có S B C ; A B C D ^ = S M O ^ = 45 o .
Ta có
A C 2 = A B 2 + B C 2 = 4 a 2 ⇒ A B = B C = a 2 . O M = 1 2 A B = a 2 2 ⇒ S O = a 2 2 . tan 45 o = a 2 2 .
Vậy V S . A B C D = 1 3 . S O . S A B C D = 1 3 . a 2 2 . a 2 2 = 2 a 3 3 .

Chọn B.
H là trung điểm của AD ;K là trung điểm của BC
Ta có ![]()
SH = KH.tan600 =
2
a
3
suy ra ![]()


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).

S D C I A K B
\(\begin{cases}\left(SIB\right)\perp\left(ABCD\right)\\\left(SIC\right)\perp\left(ABCD\right)\end{cases}\) \(\Rightarrow SI\perp\left(ABCD\right)\)
Kẻ \(IK\perp BC\left(K\in BC\right)\Rightarrow BC\perp\left(SIK\right)\)\(\Rightarrow\widehat{SKI}=60^0\)
Diện tích hình thang ABCD : \(S_{ABCD}=3a^2\)
Tổng diện tích các tam giá ABI và CDI bằng \(\frac{3a^2}{2}\) Suy ra \(S_{\Delta IBC}=\frac{3a^2}{2}\)
\(BC=\sqrt{\left(AB-CD\right)^2+AD^2}=a\sqrt{5}\)
\(\Rightarrow IK=\frac{2S_{\Delta IBC}}{BC}=\frac{3\sqrt{5}a}{5}\)
\(\Rightarrow SI=IK.\tan\widehat{SKI}=\frac{3\sqrt{15}a}{5}\)
Thể tích của khối chóp S.ABCD : \(V=\frac{1}{3}S_{ABCD}.SI=\frac{3\sqrt{15}a^2}{5}\)
Chọn C.
Gọi M là trung điểm của BC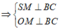
Suy ra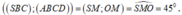
Vì AC = 2a nên