Trong không gian với hệ tọa độ Oxyz, cho điểm H 1 ; 2 ; 3 . Viết phương trình mặt phẳng (P) đi qua H, cắt các trục x ' O x , y ' O y , z ' O z lần lượt tại các điểm A, B, C A , B , C ≠ O sao cho H là trực tâm của tam giác ABC.
A. P : 2 x + y + 3 z − 13 = 0
B. P : 2 x + 3 y + z − 11 = 0
C. P : x + 2 y + 3 z − 14 = 0
D. P : x + 3 y + 2 z − 13 = 0


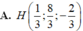
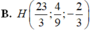
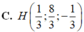
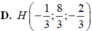
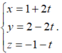
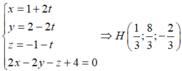
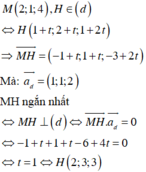

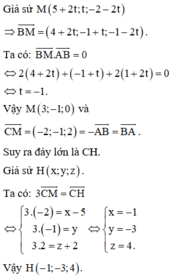

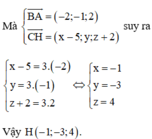

Đáp án C.
Đặt A = a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c a b c ≠ 0
Ta có H A → = a − 1 ; − 2 ; − 3 , H B → = − 1 ; b − 2 ; − 3 , B C → = 0 ; − b ; c , A C → = − a ; 0 ; c
H là trực tâm Δ A B C ⇒ H A → . B C → = 0 H B → . A C → = 0 ⇔ 2 b − 3 c = 0 a − 3 c = 0 .
Phương trình mặt phẳng có dạng x a + y b + z c = 1
⇔ x a + y a 2 + z a 3 = 1 ⇔ x + 2 y + 3 z − a = 0
Vì A B C đi qua H ⇒ 1 + 2.2 + 3.3 = a ⇔ a = 14
Vậy phương trình (P) là x + 2 y + 3 z − 14 = 0 .