Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
A. 3 a 3 8
B. a 3 4
C. a 3 8
D. 3 a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
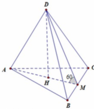
Gọi M là trung điểm của BC khi đó D M ⊥ B C A M ⊥ B C
Suy ra B C ⊥ ( D M A ) ⇒ D B C ; A B C ^ = 60 °
Lại có D M = A M = a 3 2
Dựng D H ⊥ A M ⇒ D H ⊥ ( A B C )
Khi đó V A B C D = 1 3 D H . S A B C = 1 3 D M . sin 60 ° . a 2 3 4 = a 2 3 16 .

Chọn A
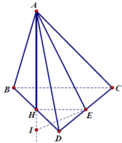
Coi như a = 1 . Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ B C D và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ A H E ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 πa 3


Chọn A
Coi như a =1. Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B ⇒ Δ A B D cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ ( B C D ) và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ ( A H E ) ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có
A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 π

Chọn B.
Phương pháp:
Ta xác định tâm mặt cầu ngoại tiếp tứ diện ABCD chính là điểm cách đều bốn đỉnh A, B, C, D.
Dựa vào tính chất tam giác cân, hai tam giác bằng nhau, tỉ số lượng giác để chứng minh các đoạn thẳng bằng nhau từ đó tìm được tâm mặt cầu.
Cách giải:
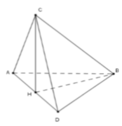
Các tam giác đều ABC và BCD có cạnh 2
⇒ B D = D C = B C = A B = A C = 2
Nên tam giác CAD cân tại C và tam giác BAD cân tại B.

Từ (1) và (2) suy ra tam giác CHB vuông cân tại H có cạnh huyền CB = 2.

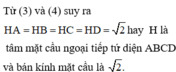
Đáp án C
Gọi H là trung điểm của BC. Ta có: A H ⊥ B C
Mặt khác A B C ⊥ B C D ⇒ A H ⊥ B C D
Lại có A H = a 3 2 ⇒ V = 1 3 A H . S B C D = 1 3 . a 3 2 . a 2 3 4 = a 3 8