Tìm tất cả các giá trị thực của tham số m để phương trình x . log 2 x − 1 + m = m . log 2 x − 1 + x có hai nghiệm thực phân biệt.
A. m > 1 v à m ≠ 2
B. m ≠ 3
C. m > 1 v à m ≠ 3
D. m > 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp:

![]() phương trình trở thành
phương trình trở thành
![]()
![]()
![]()
=> Hàm số đồng biến trên khoảng [2;+∞)
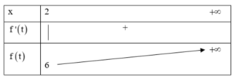
Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3

Chọn B
Để hàm số đã cho có tập xác định là R khi và chỉ khi : x2- 2x-m+ 1> 0 với mọi x
Hay
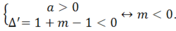
Đáp án C
Ta có: x . log 2 x − 1 + m = m . log 2 x − 1 + x
⇔ x − m . log 2 x − 1 = x − m .
⇔ x − m log 2 x − 1 − 1 ⇔ x − m = 0 log 2 x − 1 = 1 ⇔ x = m x − 1 = 2 ⇔ x = m x = 3 *
Để phương trình đã cho có 2 nghiệm phân biệt ⇔ * có nghiệm duy nhất x > 1 ; x ≠ 3. Vậy m > 1 v à m ≠ 3 là giá trị cần tìm.