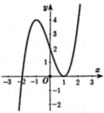
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y=f’(x) như hình bên. Số điểm cực trị của hàm số y=f(x-2017)-2018x+2019 là:
A. 3
B. 1
C. 4
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Ta có: g(x) = f(x-2017) - 2018x + 2019.
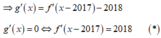
Nhận xét: tịnh tiến đồ thị hàm số y = f'(x) sang bên phải theo phương của trục hoành 2017 đơn vị ta được đồ thị hàm số y = f'(x-2017) . Do đó, số nghiệm của phương trình f'(x) = 2018 bằng số nghiệm của phương trình (*).
Dựa vào đồ thị ta thấy phương trình (*) có nghiệm đơn duy nhất hay hàm số đã cho có duy nhất 1 điểm cực trị.

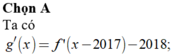
![]()
Dựa vào đồ thị hàm số y= f’(x) suy ra phương trình f’( x- 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số y= g( x) có 1 điểm cực trị

Ta có 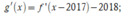
![]()
Dựa vào đồ thị hàm số y = f'(x) suy ra phương trình ![]()
có 1 nghiệm đơn duy nhất. Suy ra hàm số g(x) có 1 điểm cực trị.
Chọn A.

Ta có: f' (x - 2) = f' (x).(x-2)' = f'(x)
Do đó; đồ thị hàm số y= f’ (x) có hình dạng tương tự như trên.
Đồ thị hàm số y= f( x-2) có 3 điểm cực trị khi và chỉ khi đồ thị hàm số y= f( x) cũng có 3 điểm cực trị.
Chọn D.

Đáp án D
Phương pháp : Nhận xét : f’(x – 2) = f’(x)
Cách giải : Ta có : f’(x – 2) = (x – 2)’. f’(x) = f’(x) → Đồ thị hàm số y = f’(x) có hình dạng tương tự như trên.
Đồ thị hàm số y = f(x – 2)có 3 điểm cực trị => Đồ thị hàm số y = f(x) cũng có 3 điểm cực trị

Đáp án B
Ta có: y = f x − 2017 − 2018 x + 2019 ⇒ y ' x − 2017 x − 2017 ' − 2018
= f ' x − 2017 − 2018
Dựa vào đồ thị hàm số y = f ' x suy ra PT f ' x − 2017 = f t = 2018 có 1 nghiệm bội lẻ duy nhất
Suy ra hàm số y = f x − 2017 − 2018 x + 2019 có 1 điểm cực trị

Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
Chọn đáp án B.